| ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ | 3 |
 |
|
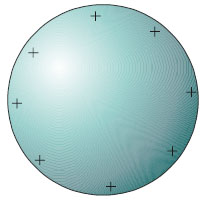
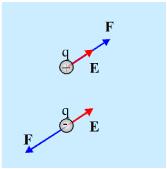 Σχ. 3.1 Εάν σ’ ένα σημείο του χώρου που καταλαμβάνει το ηλεκτροστατικό πεδίο βρεθεί ένα φορτίο q θα δεχθεί δύναμη. Εάν το q είναι θετικό η δύναμη θα είναι ομόρροπη της έντασης, ενώ αν το q είναι αρνητικό αντίρροπη. Σχ. 3.1 Εάν σ’ ένα σημείο του χώρου που καταλαμβάνει το ηλεκτροστατικό πεδίο βρεθεί ένα φορτίο q θα δεχθεί δύναμη. Εάν το q είναι θετικό η δύναμη θα είναι ομόρροπη της έντασης, ενώ αν το q είναι αρνητικό αντίρροπη.  Σχ. 3.2 Ένα ακίνητο σημειακό ηλεκτρικό φορτίο Q δημιουργεί γύρω του στο χώρο ηλεκτροστατικό πεδίο. Σχ. 3.2 Ένα ακίνητο σημειακό ηλεκτρικό φορτίο Q δημιουργεί γύρω του στο χώρο ηλεκτροστατικό πεδίο. |
3-1 ΕΙΣΑΓΩΓΗ
Το «πεδίο» μπήκε στο λεξιλόγιο των φυσικών στις αρχές του περασμένου αιώνα από τον Michael Faraday (Φαραντέι), που προσπαθούσε να εξηγήσει πώς αλληλεπιδρούν σώματα που δεν βρίσκονται σε επαφή. Πεδίο (δυνάμεων) είναι η περιοχή του χώρου μέσα στην οποία το κατάλληλο υπόθεμα δέχεται δύναμη.
Πεδίο μπορεί να δημιουργήσει μια μάζα (βαρυτικό πεδίο), ένα ακίνητο ηλεκτρικό φορτίο (ηλεκτροστατικό πεδίο) ή ένα φορτίο που κινείται (μαγνητικό πεδίο). Σε όλες τις περιπτώσεις μάς ενδιαφέρει να γνωρίζουμε τι δύναμη θα δέχεται το υπόθεμα όταν το φέρουμε σε συγκεκριμένο σημείο του πεδίου. Η ανάγκη αυτή οδήγησε στην εισαγωγή του διανυσματικού μεγέθους ένταση που την ορίσαμε ως τη δύναμη ανά μονάδα υποθέματος. Στο κεφάλαιο αυτό θα περιορισθούμε στη μελέτη του ηλεκτροστατικού και του βαρυτικού πεδίου. Το μαγνητικό πεδίο θα το δούμε ξεχωριστά, στο επόμενο κεφάλαιο. Το κοινό ανάμεσα στο ηλεκτροστατικό και το βαρυτικό πεδίο είναι ότι η δύναμη που δέχεται το υπόθεμα έχει την ίδια διεύθυνση με την ένταση και ότι το έργο της δύναμης του πεδίου δεν εξαρτάται από τη διαδρομή, είναι δηλαδή διατηρητικά πεδία. Αρχικά θα ασχοληθούμε με το νόμο του Gauss, που περιγράφει τη σχέση μεταξύ του φορτίου και του ηλεκτρικού πεδίου που δημιουργεί, στη συνέχεια με το δυναμικό, μέγεθος που περιγράφει με διαφορετικό (συμπληρωματικό) τρόπο, το ηλεκτρικό πεδίο και, τέλος, με το πεδίο βαρύτητας.
3-2 ΕΝΤΑΣΗ ΗΛΕΚΤΡΙΚΟΥ ΠΕΔΙΟΥ
Υπενθυμίζουμε ότι ένταση σ’ ένα σημείο Α ενός ηλεκτροστατικού πεδίου είναι το σταθερό πηλίκο της δύναμης που ασκείται από το πεδίο σ’ ένα φορτίο q (υπόθεμα), που θα βρεθεί στο σημείο Α, προς το φορτίο αυτό.
Η ένταση είναι διανυσματικό μέγεθος που έχει την κατεύθυνση της δύναμης που ασκείται σε ένα θετικό φορτίο. Εάν το πεδίο δημιουργείται από σημειακό φορτίο Q και η απόσταση του σημείου Α από το Q είναι r η δύναμη που θα δεχθεί το φορτίο q σύμφωνα με το νόμο
για την ένταση πεδίου σημειακού φορτίου Q ότι
Η σχέση ανάμεσα στην ένταση του ηλεκτρικού πεδίου και στις πηγές του (φορτία) μπορεί να εκφραστεί με ένα αξιοσημείωτα απλό τρόπο. Για να γίνει αυτό χρειάζεται πρώτα να ορίσουμε ένα νέο μέγεθος, που ονομάζεται ηλεκτρική ροή. |
3-3 ΗΛΕΚΤΡΙΚΗ ΡΟΗ
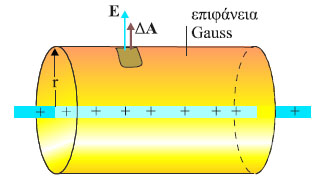
Έστω ένα ομογενές ηλεκτρικό πεδίο και μια επιφάνεια εμβαδού Α, κάθετη στις δυναμικές γραμμές του πεδίου (σχ. 3.3). Οι δυναμικές γραμμές του πεδίου σχεδιάζονται έτσι ώστε ο αριθμός τους που διαπερνά κάθετα τη μοναδιαία επιφάνεια να είναι ανάλογος με το μέτρο της έντασης του πεδίου. Ο συνολικός αριθμός των γραμμών που διαπερνούν την επιφάνεια Α είναι ανάλογος με το γινόμενο. Το γινόμενο αυτό το ονομάζουμε ηλεκτρική ροή που διέρχεται από την επιφάνεια Α και το συμβολίζουμε με ΦΕ. Αν η επιφάνεια Α δεν είναι κάθετη στις δυναμικές γραμμές, (σχ.3.4), ο αριθμός των δυναμικών γραμμών που διέρχονται από την επιφάνεια Α είναι ίσος με τον αριθμό των δυναμικών γραμμών που διέρχονται από την προβολή της επιφάνειας σε ένα επίπεδο κάθετο στις δυναμικές γραμμές.
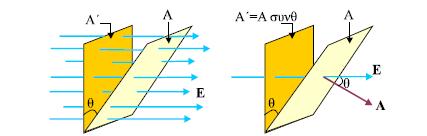
Από το σχήμα 3.4 βλέπουμε ότι A' = A' συνθ. Εφόσον ο αριθμός των δυναμικών γραμμών που διέρχονται από την Α είναι ίσος με τον αριθμό των γραμμών που διέρχονται από την Α΄, η ηλεκτρική ροή που διέρχεται από την επιφάνεια Α είναι ίση με τη ροή που διέρχεται από την επιφάνεια Α΄. Επειδή A' = A' συνθ και η ροή που διέρχεται από την επιφάνεια Α είναι
Η γωνία θ είναι η γωνία που σχηματίζει ένα διάνυσμα κάθετο στην επιφάνεια Α, ας το συμβολίσουμε με Α, με τη διεύθυνση των δυναμικών γραμμών (σχ. 3.4). Πήραμε ένα κάθετο διάνυσμα και όχι απλά την κάθετη στην επιφάνεια επειδή μια επιφάνεια έχει δύο όψεις και, αντίστοιχα, η ηλεκτρική ροή μπορεί να είναι θετική ή αρνητική. Επομένως
Η ηλεκτρική ροή ΦE που διέρχεται από μια επίπεδη επιφάνεια, εμβαδού Α, η οποία βρίσκεται μέσα σε ομογενές ηλεκτρικό πεδίο έντασης Ε, είναι ίση με
όπου θ η γωνία που σχηματίζει το κάθετο στην επιφάνεια διάνυσμα Α με τη διεύθυνση των δυναμικών γραμμών. Η ηλεκτρική ροή στο SI μετριέται σε Ν m2/C. |
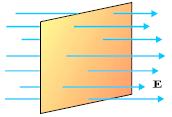 Σχ. 3.3 Η επιφάνεια είναι τοποθε-τημένη κάθετα στις δυναμικές γραμμές, ομογενούς ηλεκτρικού πεδίου. Σχ. 3.3 Η επιφάνεια είναι τοποθε-τημένη κάθετα στις δυναμικές γραμμές, ομογενούς ηλεκτρικού πεδίου.
Σχ. 3.4 Από τις επιφάνειες Α και Α΄ περνάει η ίδια ηλεκτρική ροή αφού από τις δύο επιφάνειες διέρχεται ο ίδιος αριθμός δυναμικών γραμμών.
|
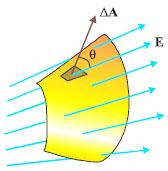 Σχ. 3.5 Για να βρούμε την ηλεκτρική ροή που διέρχεται από μια επιφάνεια τυχαίου σχήματος χωρίζουμε την επιφάνεια σε μικρά τμήματα. Σχ. 3.5 Για να βρούμε την ηλεκτρική ροή που διέρχεται από μια επιφάνεια τυχαίου σχήματος χωρίζουμε την επιφάνεια σε μικρά τμήματα.
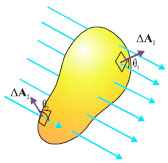 Σχ. 3.6 Κλειστή επιφάνεια μέσα σε ηλεκτρικό πεδίο. Τα κάθετα διανύσματα ΔΑ εξ ορισμού κατευθύνονται προς τα έξω. Σχ. 3.6 Κλειστή επιφάνεια μέσα σε ηλεκτρικό πεδίο. Τα κάθετα διανύσματα ΔΑ εξ ορισμού κατευθύνονται προς τα έξω.
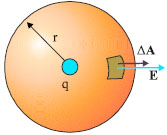 Σχ. 3.7 Το σημειακό φορτίο q βρίσκεται στο κέντρο σφαίρας ακτίνας r. Σχ. 3.7 Το σημειακό φορτίο q βρίσκεται στο κέντρο σφαίρας ακτίνας r.
|
Στη γενικότερη περίπτωση όπου η επιφάνεια Α δεν είναι επίπεδη και βρίσκεται μέσα σε ανομοιογενές ηλεκτρικό πεδίο, επειδή ούτε οι γραμμές του πεδίου τέμνουν παντού την επιφάνεια με την ίδια γωνία, ούτε η ένταση έχει παντού την ίδια τιμή, για να βρούμε την ηλεκτρική ροή πρέπει να χωρίσουμε την επιφάνεια σε μικρά τμήματα ΔA, τόσο μικρά ώστε καθένα από αυτά να μπορεί να θεωρηθεί επίπεδη επιφάνεια και σε καθένα από αυτά η ένταση του πεδίου να μπορεί να θεωρηθεί σταθερή. Η ηλεκτρική ροή ΔΦΕ που διέρχεται από μια στοιχειώδη επιφάνεια ΔΑ είναι ΔΦΕ = ΕΔA συνθ και η ηλεκτρική ροή που διέρχεται από ολόκληρη την επιφάνεια Α προκύπτει από το άθροισμα αυτών των όρων
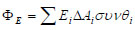 όπου Εi, θi οι τιμές των E και θ για κάθε ΔAi.
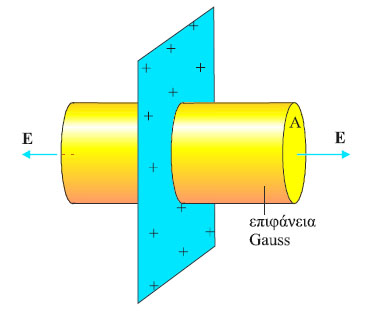
Συνήθως μας ενδιαφέρει η ηλεκτρική ροή που διέρχεται από μια κλειστή επιφάνεια. Θεωρήστε ένα ηλεκτρικό πεδίο και μέσα σ΄ αυτό μια κλειστή επιφάνεια σαν μπαλόνι (σχ. 3.6) ή με οποιοδήποτε άλλο σχήμα. Για να υπολογίσουμε την ηλεκτρική ροή που διέρχεται από αυτή την κλειστή επιφάνεια, ακολουθούμε τη διαδικασία που περιγράψαμε πιο πάνω. Χωρίζουμε την επιφάνεια σε πολύ μικρά τμήματα ΔΑ, υπολογίζουμε την ηλεκτρική ροή ΔΦΕ που διέρχεται από κάθε ένα από αυτά και, τέλος, αθροίζουμε όλους τους όρους. Το κάθετο διάνυσμα σε κάθε μικρό στοιχείο επιφάνειας ΔΑ, λαμβάνεται με φορά προς τα έξω. Αν σε ένα στοιχείο επιφάνειας όπως το ΔΑ1 οι δυναμικές γραμμές κατευθύνονται προς τα έξω, η γωνία θ1 είναι μικρότερη των 90ο, το συνημίτονο της γωνίας είναι θετικό και επομένως και η ηλεκτρική ροή ΔΦ1 που διέρχεται από το τμήμα αυτό της επιφάνειας είναι θετική. Σε άλλα τμήματα επιφάνειας, όπως το ΔΑ2 όπου οι δυναμικές γραμμές κατευθύνονται προς τα μέσα, θ2>90ο, και επομένως ΔΦ2<0. Αν από την επιφάνεια εξέρχονται περισσότερες γραμμές από όσες εισέρχονται, η ολική ροή είναι θετική ενώ αν εισέρχονται περισσότερες από όσες εξέρχονται, αρνητική. Στο σχήμα 3.6 ο αριθμός των γραμμών που εισέρχονται είναι ίσος με τον αριθμό των γραμμών που εξέρχονται, επομένως η ολική ροή είναι μηδέν.
3-4 O ΝΟΜΟΣ ΤΟΥ GAUSS (Γκάους)
Ο νόμος αυτός συνδέει την ηλεκτρική ροή που διέρχεται από μια κλειστή επιφάνεια με το φορτίο που περικλείει η επιφάνεια.
Έστω ένα σημειακό θετικό φορτίο q. Ας φανταστούμε μια σφαίρα ακτίνας r, όπως στο σχήμα 3.7, που έχει κέντρο το σημείο στο οποίο βρίσκεται το φορτίο. Θα υπολογίσουμε την ηλεκτρική ροή που διέρχεται από την σφαίρα. Γνωρίζουμε ότι η ένταση του ηλεκτρικού πεδίου στην επιφάνεια της σφαίρας έχει μέτρο
διεύθυνση ακτινική και φορά προς τα έξω.
Χωρίζουμε την επιφάνεια της σφαίρας σε στοιχειώδη τμήματα ΔΑ, τόσο μικρά ώστε το καθένα από αυτά να μπορεί να θεωρηθεί επίπεδο. Οι δυναμικές |
γραμμές του πεδίου που δημιουργεί το q τέμνουν κάθετα κάθε στοιχειώδη επιφάνεια ΔΑ και το κάθετο διάνυσμα ΔΑ σε κάθε τέτοια επιφάνεια είναι παράλληλο με τις δυναμικές γραμμές. Η ολική ροή που διέρχεται από την επιφάνεια της σφαίρας είναι
Ο όρος
Από τη σχέση αυτή προκύπτει ότι η ηλεκτρική ροή (ΦΕ) είναι ανεξάρτητη της ακτίνας r της σφαίρας που επιλέξαμε. Αυτό είναι λογικό γιατί, το πλήθος των δυναμικών γραμμών που περνά από οποιαδήποτε σφαιρική επιφάνεια με κέντρο το φορτίο είναι ίδιο ανεξάρτητα από την ακτίνα της. Στην πραγματικότητα η επιφάνεια δεν χρειάζεται να είναι σφαιρική. Από οποιαδήποτε κλειστή επιφάνεια, που περικλείει το φορτίο q, (σχ. 3.8) θα περνάει ίδιος αριθμός δυναμικών γραμμών. Επομένως, η ηλεκτρική ροή για κάθε κλειστή επιφάνεια που περικλείει το φορτίο q είναι ίση με αυτή που βρήκαμε για τη σφαίρα, δηλαδή
Το συμπέρασμα στο οποίο καταλήξαμε γενικεύεται και στην περίπτωση που έχουμε πολλά σημειακά φορτία, ή φορτισμένα σώματα. Με την αρχή της επαλληλίας αποδεικνύεται ότι η ηλεκτρική ροή που διέρχεται από μια οποιαδήποτε κλειστή επιφάνεια είναι ίση με Qεγκ/εο όπου Qεγκ το φορτίο που περικλείεται από την κλειστή επιφάνεια. Η παραπάνω πρόταση αποτελεί το νόμο του Gauss για το ηλεκτρικό πεδίο. Σύμφωνα με αυτόν
η ηλεκτρική ροή που διέρχεται από μια κλειστή επιφάνεια ισούται με το πηλίκο του ολικού φορτίου που περικλείει η επιφάνεια, προς τη σταθερά εο.
Την κλειστή επιφάνεια που επιλέγουμε για να εφαρμόσουμε το νόμο του Gauss θα την ομομάζουμε επιφάνεια Gauss. Κατά την εφαρμογή του νόμου του Gauss πρέπει να είμαστε προσεκτικοί. Ενώ το φορτίο Qεγκστη σχέση (3.4) είναι το φορτίο που βρίσκεται μέσα στην επιφάνεια Gauss, το Ε είναι το ολικό ηλεκτρικό πεδίο που οφείλεται τόσο σε φορτία που βρίσκονται μέσα στην επιφάνεια όσο και σε φορτία που βρίσκονται έξω από αυτήν.
Ο νόμος του Gauss είναι θεμελιώδους σημασίας στην ηλεκτροστατική. Η σημασία του είναι ανάλογη με αυτήν του νόμου του Coulomb. Στην πραγματικότητα ο νόμος του Gauss και ο νόμος του Coulomb δεν είναι δυο ανεξάρτητοι φυσικοί νόμοι, αλλά ο ίδιος νόμος που εκφράζεται με δύο διαφορετικούς τρόπους.
Στη συνέχεια θα δούμε ότι ο νόμος του Gauss δίνει εύκολα την ένταση του ηλεκτρικού πεδίου σε περιπτώσεις όπου έχουμε συμμετρική κατανομή φορτίου. |
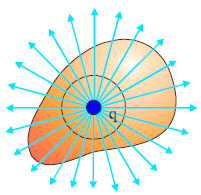 Σχ. 3.8 H ηλεκτρική ροή που διέρχεται από τις δύο επιφάνειες είναι ίδια. Σχ. 3.8 H ηλεκτρική ροή που διέρχεται από τις δύο επιφάνειες είναι ίδια.
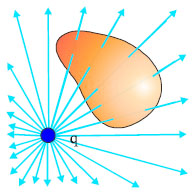 Σχ. 3.9 Το φορτίο q βρίσκεται έξω από την επιφάνεια. Οι δυναμικές γραμμές του πεδίου που δημιουργεί και εισέρχονται σ’ αυτή εξέρχονται από κάποιο άλλο σημείο απ’ αυτή. Η συνολική ηλεκτρική ροή που περνάει από την επιφάνεια είναι ίση με μηδέν. Σχ. 3.9 Το φορτίο q βρίσκεται έξω από την επιφάνεια. Οι δυναμικές γραμμές του πεδίου που δημιουργεί και εισέρχονται σ’ αυτή εξέρχονται από κάποιο άλλο σημείο απ’ αυτή. Η συνολική ηλεκτρική ροή που περνάει από την επιφάνεια είναι ίση με μηδέν.
 Εικ. 3.1 Karl Friedrich Gauss. (1777-1855). Γερμανός, ένας από τους μεγαλύτερους μαθηματικούς όλων των αιώνων. Εικ. 3.1 Karl Friedrich Gauss. (1777-1855). Γερμανός, ένας από τους μεγαλύτερους μαθηματικούς όλων των αιώνων. |
|
Εφαρμογές του νόμου του Gauss
Όπως είπαμε, με το νόμο του Gauss μπορούμε να υπολογίσουμε εύκολα την ένταση του ηλεκτρικού πεδίου σε περιπτώσεις που το ηλεκτρικό φορτίο κατανέμεται συμμετρικά. Στις περιπτώσεις αυτές επιλέγουμε μια επιφάνεια (επιφάνεια Gauss) που έχει την ίδια συμμετρία με εκείνη της κατανομής του φορτίου.
|
ΠΑΡΑΔΕΙΓΜΑ 3.1 |
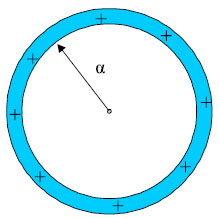
Ένα σφαιρικό κέλυφος που θεωρούμε ότι έχει αμελητέο πάχος (σχ.3.10) έχει ακτίνα α και φέρει φορτίο Q, ομοιόμορφα κατανεμημένο στην επιφάνειά του. Βρείτε την ένταση του ηλεκτρικού πεδίου στο εξωτερικό και στο εσωτερικό του σφαιρικού κελύφους.
Απάντηση:
Επειδή το φορτίο είναι ομοιόμορφα κατανεμημένο στην επιφάνεια του κελύφους, το πεδίο που δημιουργεί το κέλυφος έχει ακτινική διεύθυνση και η ένταση έχει την ίδια τιμή σε όλα τα σημεία που απέχουν το ίδιο από το κέντρο του κελύφους. Για τους λόγους αυτούς επιλέγουμε ως επιφάνεια Gauss μια σφαιρική επιφάνεια, ομόκεντρη με το κέλυφος.
Α) Η επιφάνεια Gauss έχει ακτίνα r μεγαλύτερη ή ίση της ακτίνας του κελύφους, r ≥ α. Χωρίζουμε την επιφάνεια σε πολύ μικρά τμήματα. Έστω ένα από αυτά, εμβαδού ΔΑ. Η κάθετη ΔΑ στην επιφάνεια ΔΑ και η ένταση του πεδίου σ΄ αυτή την περιοχή, έχουν την ίδια κατεύθυνση, (σχ. 3.11) επομένως η ροή που διέρχεται από την επιφάνεια ΔΑ είναι
Το ίδιο ισχύει και για κάθε άλλο τμήμα ΔΑ της επιφάνειας Gauss. Άρα η συνολική ροή είναι
Όμως από το νόμο του Gauss έχουμε
Από (3.5) και (3.6) έχουμε
Αυτή όμως είναι η σχέση που δίνει την ένταση του πεδίου που δημιουργεί ένα σημειακό φορτίο Q, σε απόσταση r. Επομένως ο σφαιρικός φλοιός συμπεριφέρεται, στον εξωτερικό του χώρο, σαν να ήταν ένα σημειακό φορτίο συγκεντρωμένο στο κέντρο του.
Ας δούμε όμως τι συμβαίνει στο εσωτερικό |
 Σχ. 3.10 Το ηλεκτρικό φορτίο είναι ομοιόμορφα κατανεμημένο στο σφαιρικό κέλυφος. Σχ. 3.10 Το ηλεκτρικό φορτίο είναι ομοιόμορφα κατανεμημένο στο σφαιρικό κέλυφος. 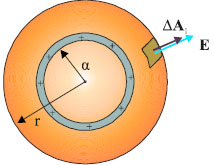 Σχ. 3.11 H επιφάνεια Gauss είναι σφαίρα ομόκεντρη με το κέλυφος με ακτίνα μεγαλύτερη ή ίση της ακτίνας του κελύφους. Σχ. 3.11 H επιφάνεια Gauss είναι σφαίρα ομόκεντρη με το κέλυφος με ακτίνα μεγαλύτερη ή ίση της ακτίνας του κελύφους. |
Β) Επιλέγουμε και πάλι μια σφαιρική επιφάνεια Gauss ομόκεντρη με το κέλυφος που τώρα έχει ακτίνα r < α. Αν, όπως και πριν, φανταστούμε την επιφάνεια χωρισμένη σε στοιχειώδη τμήματα, θα καταλήξουμε πάλι στη σχέση
Σύμφωνα με το νόμο του Gauss
Από (3.7) και (3.8) προκύπτει Ε=0
Δηλαδή στο εσωτερικό του κελύφους δεν υπάρχει ηλεκτρικό πεδίο. |
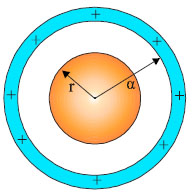 Σχ. 3.12 Η επιφάνεια Gauss είναι σφαίρα ομόκεντρη με το κέλυφος και με μικρότερη ακτίνα Σχ. 3.12 Η επιφάνεια Gauss είναι σφαίρα ομόκεντρη με το κέλυφος και με μικρότερη ακτίνα |
Παρατήρηση
Σε κάθε σώμα υπάρχει και θετικό και αρνητικό φορτίο. Στα ηλεκτρικά ουδέτερα σώματα, το ποσό του θετικού φορτίου είναι ίσο με το ποσό του αρνητικού φορτίου. Αν ένα σώμα είναι φορτισμένο πλεονάζει το θετικό ή το αρνητικό φορτίο. Σε ένα φορτισμένο αγωγό οι απωστικές δυνάμεις μεταξύ των φορτίων που πλεονάζουν είναι ισχυρότερες από τις ελκτικές δυνάμεις που δέχονται από τα φορτία που έχουν αντίθετο πρόσημο. Έτσι τα φορτία που πλεονάζουν τείνουν να απομακρυνθούν μεταξύ τους και συγκεντρώνονται στην επιφάνεια του αγωγού.1 Αν ο αγωγός είναι σφαιρικός το πλεονάζον φορτίο κατανέμεται ομοιόμορφα στην επιφάνεια του αγωγού. Επομένως το πεδίο που δημιουργεί ένας στατικά φορτισμένος σφαιρικός αγωγός είναι όμοιο με το πεδίο ενός φορτισμένου σφαιρικού κελύφους. |
 Σχ. 3.12 Όλο το φορτίο του σφαιρικού αγωγού βρίσκεται στην επιφάνειά του. Εξωτερικά ο αγωγός συμπεριφέρεται σαν όλο του το φορτίο να είναι συγκεντρωμένο στο κέντρο του (σαν σημειακό φορτίο). Στο εσωτερικό του αγωγού το πεδίο είναι μηδέν. Σχ. 3.12 Όλο το φορτίο του σφαιρικού αγωγού βρίσκεται στην επιφάνειά του. Εξωτερικά ο αγωγός συμπεριφέρεται σαν όλο του το φορτίο να είναι συγκεντρωμένο στο κέντρο του (σαν σημειακό φορτίο). Στο εσωτερικό του αγωγού το πεδίο είναι μηδέν. |
ΠΑΡΑΔΕΙΓΜΑ 3.2 |
Ένα πολύ μεγάλο (απείρου μήκους) σύρμα είναι ομοιόμορφα φορτισμένο. Αν το φορτίο που φέρει ανά μονάδα μήκους είναι λ (ονομάζεται και «γραμμική πυκνότητα φορτίου»), να βρεθεί η ένταση του ηλεκτρικού πεδίου που δημιουργεί.
Απάντηση:
Για λόγους συμμετρίας, το πεδίο που δημιουργεί ένα τέτοιο σύρμα είναι ακτινικό και η τιμή της έντασης είναι ίδια σε όλα τα σημεία που απέχουν το ίδιο από το σύρμα. Τα σημεία αυτά αποτελούν μια κυλινδρική επιφάνεια. Για να εκμεταλλευτούμε τη συμμετρία του πεδίου, επιλέγουμε ως επιφάνεια Gauss την επιφάνεια κυλίνδρου που έχει άξονα το φορτισμένο σύρμα, μήκος L και βάσεις που έχουν ακτίνα r. H ένταση του ηλεκτρικού πεδίου που δημιουργεί το σύρμα είναι κάθετη και έχει το ίδιο μέτρο σε κάθε σημείο της κυρτής επιφάνειας του κυλίνδρου. 1 Στην πραγματικότητα τα φορτία που μετακινούνται στον αγωγό είναι τα ελεύθερα ηλεκτρόνια. |
Σχ. 3.14 Επιλέγουμε επιφάνεια Gauss μια κυλινδρική επιφάνεια ομοαξονική με το σύρμα.
Η ροή που διαπερνά τις βάσεις του κυλίνδρου είναι μηδέν, γιατί η ένταση είναι παράλληλη με τις πλευρές αυτές. Αν χωρίσουμε την κυρτή επιφάνεια του κυλίνδρου σε στοιχειώδη τμήματα, η κάθετη σε κάθε τέτοιο στοιχειώδες τμήμα είναι παράλληλη με την ένταση του πεδίου. Η ολική ροή που διέρχεται από τον κύλινδρο είναι:
Το ολικό φορτίο που περικλείει η κυλινδρική επιφάνεια είναι L λ. Επομένως ο νόμος του Gauss γράφεται
Αντικαθιστώντας την ηλεκτρική ροή από την (3.9) έχουμε
η ένταση σε ένα σημείο του πεδίου που δημιουργεί το σύρμα είναι αντίστροφα ανάλογη της απόστασης από αυτό
ΠΑΡΑΔΕΙΓΜΑ 3.3
Έστω ένα επίπεδο φύλλο άπειρων διαστάσεων, που είναι ομοιόμορφα φορτισμένο. Το φορτίο ανά μονάδα επιφάνειας είναι σ (λέγεται και «επιφανειακή πυκνότητα φορτίου»). Ζητάμε την ένταση του ηλεκτρικού πεδίου που δημιουργεί η φορτισμένη επιφάνεια.
Απάντηση:
Η ένταση του πεδίου, για λόγους συμμετρίας, έχει διεύθυνση κάθετη στο επίπεδο του φορτισμένου φύλλου και το ίδιο μέτρο σε δύο σημεία που απέχουν εξίσου από το φορτισμένο φύλλο και βρίσκονται σε αντίθετες πλευρές. Επιλέγουμε ως επιφάνεια Gauss την επιφάνεια ενός κυλίνδρου που έχει τον άξονά του κάθετο στο φορτισμένο φύλλο και τις δύο βάσεις του, εμβαδού Α, να ισαπέχουν από το φορτισμένο επίπεδο. |
 Σχ. 3.15 Επιλέγουμε επιφάνεια Gauss μια κυλινδρική επιφάνεια. Ο άξονας του κυλίνδρου είναι κάθετος στο φορτισμένο φύλλο και οι βάσεις του ισαπέχουν από αυτό. Σχ. 3.15 Επιλέγουμε επιφάνεια Gauss μια κυλινδρική επιφάνεια. Ο άξονας του κυλίνδρου είναι κάθετος στο φορτισμένο φύλλο και οι βάσεις του ισαπέχουν από αυτό.
Η ροή που διέρχεται από την κυρτή επιφάνεια του κυλίνδρου είναι μηδέν αφού κάθε στοιχειώδες τμήμα της είναι παράλληλο με τις δυναμικές γραμμές του πεδίου. Η ένταση του ηλεκτρικού πεδίου είναι κάθετη στις βάσεις του κυλίνδρου και το μέτρο της είναι ίδιο και στις δύο βάσεις. Η ροή που διέρχεται από κάθε βάση είναι ΕΑ. Η ολική ροή που διέρχεται από τον κύλινδρο είναι
Το ολικό φορτίο που περιέχεται στην κυλινδρική επιφάνεια είναι σΑ. Σύμφωνα με τον νόμο του Gauss
Από (3.11) και (3.10) προκύπτει
Από το αποτέλεσμα προκύπτει ότι η τιμή της έντασης είναι ανεξάρτητη της απόστασης από το φορτισμένο φύλλο.
Το ηλεκτρικό πεδίο που δημιουργεί το φορτισμένο φύλλο απείρων διαστάσεων είναι ομογενές σε κάθε περιοχή του χώρου που ορίζεται από αυτό.
Προσοχή: Η θερμότητα δεν πρέπει να συγχέεται με τη θερμοκρασία. Η θερμότητα είναι ενέργεια ενώ η θερμοκρασία είναι το μέγεθος που επινοήσαμε για να μετράμε αντικειμενικά πόσο ζεστό ή κρύο είναι ένα σώμα.
|
 Σχ. 2.16 ΣΟ χώρος γύρω από τα φορτισμένα σώματα είναι ηλεκτρικό πεδίο. Το ηλεκτρικό πεδίο ασκεί δύναμη F σε ένα φορτίο. Σχ. 2.16 ΣΟ χώρος γύρω από τα φορτισμένα σώματα είναι ηλεκτρικό πεδίο. Το ηλεκτρικό πεδίο ασκεί δύναμη F σε ένα φορτίο.
|
3-5 ΔΥΝΑΜΙΚΟ – ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
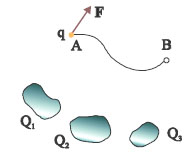
Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.3.16). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα σωματίδιο με φορτίο q, το πεδίο θα ασκήσει στο φορτίο δύναμη F=Eq. Αν μετακινήσουμε το φορτίο q από το σημείο Α, σε ένα άλλο σημείο Β, του ηλεκτρικού πεδίου, σε όλη τη διάρκεια της διαδρομής το ηλεκτρικό πεδίο ασκεί στο φορτίο q δύναμη. H δύναμη αυτή, κατά τη μετακίνηση του φορτίου, παράγει ή καταναλώνει έργο. Αποδεικνύεται ότι το έργο της δύναμης του πεδίου κατά τη μετακίνηση του φορτίου q, από το σημείο Α στο σημείο Β του ηλεκτρικού πεδίου, είναι το ίδιο, όποια διαδρομή και αν επιλέξουμε (τέτοια πεδία ονομάζονται διατηρητικά). Αν μάλιστα το έργο αυτό διαιρεθεί με το φορτίο που μετακινείται, τότε το πηλίκο W/q, που εκφράζει το έργο ανά μονάδα φορτίου, είναι ανεξάρτητο όχι μόνο από τη διαδρομή αλλά και από το φορτίο που μετακινείται κάθε φορά. Την ιδιότητα αυτή του ηλεκτρικού πεδίου την εκμεταλλευόμαστε για να ορίσουμε ένα νέο μέγεθος, το δυναμικό. Συγκεκριμένα :
Ονoμάζουμε δυναμικό του ηλεκτρικού πεδίου σε ένα σημείο του Α το σταθερό πηλίκο του έργου της δύναμης που ασκεί το πεδίο σε φορτίο q, κατά τη μετακίνηση του φορτίου q από το σημείο Α στο άπειρο, προς το φορτίο που μετακινείται.
To δυναμικό είναι μονόμετρο μέγεθος. Η μονάδα του στο σύστημα SI είναι το 1 Volt (V), που ισοδυναμεί με 1 J/C.
Τη διαφορά των δυναμικών μεταξύ δύο σημείων Α και Β την ονομάζουμε διαφορά δυναμικού ή τάση των σημείων Α και Β.
Η διαφορά δυναμικού, VA -V B ανάμεσα σε δύο σημεία Α και Β του ηλεκτρικού πεδίου είναι ίση με το πηλίκο του έργου που παράγει ή καταναλώνει η δύναμη του πεδίου κατά τη μετακίνηση ενός φορτίου q από το σημείο Α στο σημείο Β προς το φορτίο q.
Το έργο της δύναμης του πεδίου όταν μετατοπίζεται φορτίο q ανάμεσα σε δύο σημεία που παρουσιάζουν διαφορά δυναμικού, είναι
Αν το φορτίο που μετακινείται είναι το στοιχειώδες φορτίο (e=1,6x10-19 C ) και η διαφορά δυναμικού που παρουσιάζουν τα σημεία Α και Β είναι 1V, το έργο της δύναμης του πεδίου είναι W=1V·1,6x10-19 C=1,6x10-19J. Το έργο αυτό το ονομάζουμε ηλεκτρονιοβόλτ και το συμβολίζουμε με 1 eV.
|
Η διαφορά δυναμικού εκφράζει το έργο της δύναμης του πεδίου, ανά μονάδα φορτίου, κατά τη μετακίνηση ενός φορτίου μέσα στο ηλεκτρικό πεδίο. Επειδή το δυναμικό σχετίζεται με το έργο, είναι ένα μέγεθος εξαιρετικά χρήσιμο για τη μελέτη ενός προβλήματος από ενεργειακή άποψη.
Αν αφήσουμε σε ένα σημείο Α του ηλεκτρικού πεδίου ένα θετικό φορτίο αυτό θα κινηθεί στην κατεύθυνση της δύναμης που δέχεται από το πεδίο. Το έργο αυτής της δύναμης είναι θετικό και επομένως η διαφορά δυναμικού μεταξύ του σημείου Α και ενός άλλου σημείου Β στη διαδρομή του φορτίου (VA - VB) είναι θετική, δηλαδή το δυναμικό στο σημείο Β είναι μικρότερο από το δυναμικό στο σημείο Α. Το ηλεκτρικό πεδίο αναγκάζει τα θετικά φορτία που αφήνονται (υo=0) σε ένα σημείο του να κινούνται στην κατεύθυνση στην οποία τα δυναμικά μικραίνουν. Αντίθετα, τα αρνητικά φορτία κινούνται προς την κατεύθυνση στην οποία τα δυναμικά αυξάνονται.
Το δυναμικό πεδίου που οφείλεται σε σημειακό φορτίο
Αποδεικνύεται ότι το δυναμικό του πεδίου που οφείλεται σε σημειακό φορτίο Q, σε ένα σημείο που απέχει από το φορτίο απόσταση r, έχει τιμή
Παρατηρήσεις
Δυναμικό φορτισμένου αγωγού
Ένας στατικά φορτισμένος αγωγός, δηλαδή ένας αγωγός που φέρει ακίνητα φορτία, έχει παντού το ίδιο δυναμικό, διότι αν το δυναμικό δεν ήταν ίδιο παντού δε θα είχαμε φορτία ακίνητα -σε ισορροπία- αλλά φορτία σε κίνηση.
|
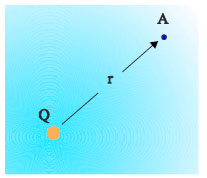 Σχ. 3.17 Σημειακό φορτίο Q δημιουργεί στο χώρο ηλεκτρικό πεδίο. Το δυναμικό στο σημείο Α του πεδίου είναι Σχ. 3.17 Σημειακό φορτίο Q δημιουργεί στο χώρο ηλεκτρικό πεδίο. Το δυναμικό στο σημείο Α του πεδίου είναι
|
ΠΑΡΑΔΕΙΓΜΑ 3.4 |
Στις κορυφές Β και Γ νοητού ισόπλευρου τριγώνου ΑΒΓ πλευράς α, έχουν τοποθετηθεί τα σημειακά φορτία Q και –2Q, αντίστοιχα. Να υπολογιστούν:
|
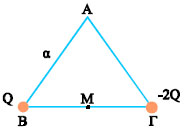 Σχ. 3.18 Σχ. 3.18 |
Απάντηση:
ΠΑΡΑΔΕΙΓΜΑ 3.5
Ένα πρωτόνιο βάλλεται από μεγάλη απόσταση, με ταχύτητα υ=400 m/s, προς ακίνητο πυρήνα άνθρακα. Να υπολογιστεί η ελάχιστη απόσταση από τον πυρήνα στην οποία θα φτάσει το πρωτόνιο. Δίνονται: το στοιχειώδες φορτίο e = 1,6 x 10-19C, η μάζα του πρωτονίου mP = 1,6 x 10-27 kg, ο ατομικός αριθμός του άνθρακα: 6, η σταθερά του Coulomb Κc = 9 x 109 Ν m2 /C2. Θα υποθέσετε ότι ο πυρήνας παραμένει ακίνητος σε όλη τη διάρκεια του φαινομένου.
Απάντηση:
Το φορτίο του πυρήνα του άνθρακα είναι Q=6e. Στο σημείο Α, το πλησιέστερο προς τον πυρήνα σημείο στο οποίο φτάνει το πρωτόνιο, η ταχύτητά του στιγμιαία μηδενίζεται. Εφαρμόζουμε το θεώρημα έργου - ενέργειας για το πρωτόνιο, κατά την κίνησή του από το άπειρο μέχρι τη θέση Α.
όπου το δυναμικό που δημιουργεί ο πυρήνας στο σημείο Α. Αν το σημείο Α απέχει από τον πυρήνα απόσταση r
Αντικαθιστώντας τις (3.19) και (3.20) στην (3.18) έχουμε
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3-6 Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΠΟΛΛΩΝ
ΣΗΜΕΙΑΚΩΝ ΦΟΡΤΙΩΝ
Έστω ένα σύστημα που αποτελείται από τρία σημειακά φορτία, τα q1, q2 και q3 (σχ. 3.19). Ας ονομάσουμε τις θέσεις τους Α, Β, Γ και τις μεταξύ τους αποστάσεις α, β και γ, όπως στο σχήμα 3.19. Η ενέργεια που έχει η ομάδα των τριών φορτίων είναι ίση με το έργο που απαιτείται για να μεταφερθούν αυτά τα φορτία από πολύ μακριά και να τοποθετηθούν στις θέσεις τους. Ας συγκεντρώσουμε τα φορτία μεταφέροντάς τα ένα - ένα.
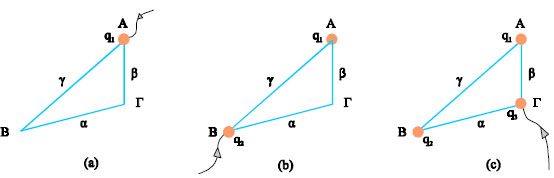 Σχ. 3.20 Αρχικά τοποθετούμε το q1 στο σημείο Α(a), στη συνέχεια το q2 στο σημείο Β(b) και τέλος το q3 στο Γ(c). Σχ. 3.20 Αρχικά τοποθετούμε το q1 στο σημείο Α(a), στη συνέχεια το q2 στο σημείο Β(b) και τέλος το q3 στο Γ(c).
Το φορτίο q1 μπορεί να μεταφερθεί στο σημείο Α χωρίς παραγωγή ή δαπάνη έργου. Στη συνέχεια, μεταφέρουμε το q2 στο σημείο Β. Το φορτίο q2, κινείται μέσα στο πεδίο που έχει δημιουργηθεί από το q1. Το έργο που απαιτείται για να μεταφερθεί το φορτίο είναι αντίθετο του έργου της δύναμης του πεδίου.
Ας μεταφέρουμε τώρα το q3. Το έργο της δύναμης που απαιτείται για την μεταφορά του είναι αντίθετο του έργου της δύναμης του πεδίου που δημιουργούν τα q1 και q2 μαζί.
Επειδή το δυναμικό στο σημείο Γ οφείλεται στα φορτία q1 και q2 και είναι
|
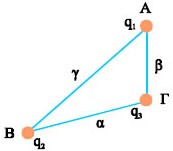 Σχ. 3.19 Σύστημα τριών σημειακών φορτίων. Σχ. 3.19 Σύστημα τριών σημειακών φορτίων.
|
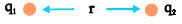 Σχ. 3.21 Το σύστημα δύο σημειακών φορτίων που απέχουν μεταξύ τους απόσταση r έχει δυναμική ενέργεια. Σχ. 3.21 Το σύστημα δύο σημειακών φορτίων που απέχουν μεταξύ τους απόσταση r έχει δυναμική ενέργεια. |
η σχέση (3.22) γίνεται
Το συνολικό έργο, που απαιτείται για να συγκεντρώσουμε τα τρία φορτία, προκύπτει από το άθροισμα των σχέσεων (3.21) και (3.23) και είναι
Τόση είναι και η δυναμική ενέργεια του συστήματος
Να σημειώσουμε ότι η δυναμική ενέργεια που υπολογίσαμε ανήκει στο σύστημα των φορτίων. Δεν υπάρχει κανένας λογικός τρόπος να αποδώσουμε μέρος αυτής της ενέργειας σε κάποιο από τα φορτία.
Στην περίπτωση δύο σημειακών φορτίων q1 και q2 που απέχουν απόσταση r η δυναμική ενέργεια του συστήματος είναι
Από τη σχέση (3.26) προκύπτει ότι αν τα φορτία είναι ομώνυμα η δυναμική τους ενέργεια είναι θετική. Αυτό είναι συνέπεια των απωστικών δυνάμεων που αναπτύσσονται μεταξύ τους. Για να μεταφερθούν τα φορτία από πολύ μακριά και να πλησιάσουν σε απόσταση r πρέπει να προσφερθεί έργο στο σύστημα. Αντίθετα, αν τα φορτία είναι ετερώνυμα έλκονται και απαιτείται αρνητικό έργο για να τοποθετηθούν σε απόσταση r μεταξύ τους. Επομένως η δυναμική τους ενέργεια είναι αρνητική.
|
ΠΑΡΑΔΕΙΓΜΑ 3.6
Σφαιρίδιο μάζας m1= 22 x 10-5kg φορτισμένο με θετικό φορτίο q1= 11 x 10-7C βάλλεται με αρχική ταχύτητα υo= 30 m/s προς δεύτερο σφαιρίδιο με μάζα m2= 2m1 και φορτίο q2= 2q1 που είναι αρχικά ακίνητο σε απόσταση d = 2m από το πρώτο. Αν τα σφαιρίδια βρίσκονται πάνω σε οριζόντιο, λείο και μονωτικό δάπεδο να βρεθεί η ελάχιστη απόσταση L στην οποία θα πλησιάσουν. Δίνεται Κc = 9 x 109 Ν m2 /C2.
Απάντηση:
Η μηχανική ενέργεια του συστήματος διατηρείται. Αν θεωρήσουμε ως αρχική θέση τη θέση από την οποία βάλλεται το σφαιρίδιο m1 και ως τελική τη θέση που τα σφαιρίδια βρίσκονται στην ελάχιστη απόσταση μεταξύ τους θα ισχύει
Επειδή στο σύστημα δεν ασκούνται εξωτερικές δυνάμεις, η ορμή του συστήματος διατηρείται.
Αντικαθιστώντας τις (3.19) και (3.20) στην (3.18) έχουμε
Θεωρώντας θετική κατεύθυνση την αρχική φορά κίνησης του m1 η παραπάνω σχέση γράφεται αλγεβρικά
αντικαθιστώντας στην (3.27) και λύνοντας ως προς L προκύπτει
Παρατήρηση: Για τη λύση του προβλήματος χρησιμοποιήσαμε την αρχή διατήρησης της μηχανικής ενέργειας. Όμως, το πεδίο που δημιουργείται από κινούμενα φορτία είναι ηλεκτρομαγνητικό πεδίο και όταν, όπως συμβαίνει στο πρόβλημά μας τα φορτία επιταχύνονται ένα μέρος της ενέργειάς τους μεταφέρεται με τη μορφή ηλεκτρομαγνητικής ακτινοβολίας στο περιβάλλον |
3-7 ΣΧΕΣΗ ΕΝΤΑΣΗΣ ΚΑΙ ΔΙΑΦΟΡΑΣ ΔΥΝΑΜΙΚΟΥ
ΣΤΟ ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ
Η ένταση και το δυναμικό είναι μεγέθη που περιγράφουν το ηλεκτρικό πεδίο. Λογικό είναι, λοιπόν, τα δύο μεγέθη να σχετίζονται. Πράγματι υπάρχει μια γενική σχέση ανάμεσα στην ένταση και το δυναμικό η οποία όμως απαιτεί μαθηματικά που ξεφεύγουν από το επίπεδο αυτού του βιβλίου. Εμείς θα δούμε πώς σχετίζονται αυτά τα δύο μεγέθη στην περίπτωση που το ηλεκτρικό πεδίο είναι ομογενές.
Έστω το ομογενές ηλεκτρικό πεδίο του σχήματος 3.23. Αν στο σημείο Α αφεθεί ένα θετικό φορτίο q, θα δεχτεί δύναμη F=Εq στην κατεύθυνση των δυναμικών γραμμών και θα κινηθεί κατά μήκος της δυναμικής γραμμής στην οποία βρίσκεται. Έστω ότι Β είναι ένα άλλο σημείο, πάνω στην ίδια δυναμική γραμμή που απέχει από το σημείο Α απόσταση x. Το έργο της δύναμης F κατά τη μετακίνηση του φορτίου από το σημείο Α στο σημείο Β είναι
Γνωρίζουμε όμως ότι W = (VA - VB)q Έτσι, η σχέση (3.28) γίνεται
όπου με V συμβολίσαμε τη διαφορά δυναμικού των σημείων Α και Β. |
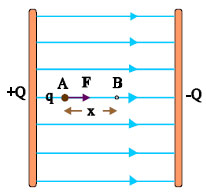 Σχ. 3.23 Θετικό σημειακό φορτίο q αφήνεται στο σημείο Α ομογενούς ηλεκτρικού πεδίου. Το πεδίο ασκεί δύναμη που έχει την κατεύθυνση των δυναμικών γραμμών. Σχ. 3.23 Θετικό σημειακό φορτίο q αφήνεται στο σημείο Α ομογενούς ηλεκτρικού πεδίου. Το πεδίο ασκεί δύναμη που έχει την κατεύθυνση των δυναμικών γραμμών. |
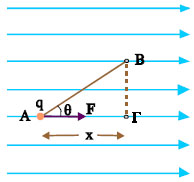 Σχ. 3.24 Το έργο της δύναμης του πεδίου κατά τη μετακίνησή του από το Α στο Β είναι ίσο με το έργο κατά τη μετακίνησή του από το Α στο Γ. Σχ. 3.24 Το έργο της δύναμης του πεδίου κατά τη μετακίνησή του από το Α στο Β είναι ίσο με το έργο κατά τη μετακίνησή του από το Α στο Γ.
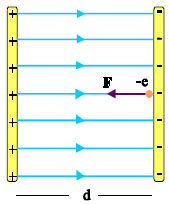 Σχ. 3.25 Ένα ηλεκτρόνιο αφήνεται μέσα σε ομογενές ηλεκτρικό πεδίο. Σχ. 3.25 Ένα ηλεκτρόνιο αφήνεται μέσα σε ομογενές ηλεκτρικό πεδίο.
|
Ας εξετάσουμε τώρα τη γενικότερη περίπτωση στην οποία τα σημεία Α και Β δεν βρίσκονται πάνω στην ίδια δυναμική γραμμή (σχ. 3.24). Αν αναγκάσουμε ένα φορτίο q, να κινηθεί από το σημείο Α στο Β κατά μήκος της ευθείας ΑΒ το έργο της δύναμης του πεδίου είναι
και επειδή W = (VA - VB)q προκύπτει πάλι η σχέση (3.29)
Γενικεύοντας το συμπέρασμα της (3.29) μπορούμε να πούμε ότι η ένταση στο ομογενές ηλεκτρικό πεδίο είναι ίση με το πηλίκο της διαφοράς δυναμικού δύο οποιωνδήποτε σημείων του ηλεκτρικού πεδίου προς την απόστασή τους x, μετρημένη κατά μήκος μιας δυναμικής γραμμής.
3-8 ΚΙΝΗΣΕΙΣ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙΔΙΩΝ ΣΕ
ΟΜΟΓΕΝΕΣ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ
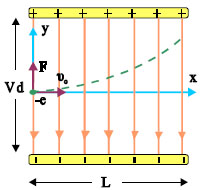
Δύο παράλληλες μεταλλικές πλάκες φορτισμένες με αντίθετα φορτία, όπως στο σχήμα, δημιουργούν ανάμεσά τους ομογενές ηλεκτρικό πεδίο. Αν μέσα σ’ αυτό το πεδίο βρεθεί ένα φορτισμένο σωματίδιο θα δεχτεί σταθερή δύναμη F=Eq και θα αποκτήσει σταθερή επιτάχυνση α = Eq/m.
Α. Κίνηση χωρίς αρχική ταχύτητα
Ένα ηλεκτρόνιο (σχ. 3.25) αφήνεται πολύ κοντά στην αρνητική πλάκα. Το ηλεκτρόνιο θα δεχτεί από το πεδίο δύναμη σταθερού μέτρου F = Ee (E: η ένταση του πεδίου και e: το στοιχειώδες ηλεκτρικό φορτίο) αντίρροπη της Ε και θα κινηθεί ευθύγραμμα ομαλά επιταχυνόμενα, με επιτάχυνση α = F / me Η κίνηση του ηλεκτρονίου περιγράφεται από τις σχέσεις
από τις οποίες μπορούμε να υπολογίσουμε:
1. Πόσο χρόνο χρειάζεται το ηλεκτρόνιο για να φτάσει στην απέναντι πλάκα;
|
2. Με ποια ταχύτητα φτάνει το ηλεκτρόνιο στη θετική πλάκα;
Αντικαθιστώντας στη σχέση υ = at το χρόνο που βρήκαμε παραπάνω βρίσκουμε
Ας κάνουμε μια αριθμητική εφαρμογή για να δούμε για ποιας τάξης μεγέθους ταχύτητες και χρόνους μιλάμε. Αν η διαφορά δυναμικού ανάμεσα στις μεταλλικές πλάκες είναι V = 1kV και η απόσταση μεταξύ τους d = 5 mm η ένταση του πεδίου στο εσωτερικό του θα είναι Ε=2 x 105 N/C, η δύναμη που θα δεχθεί το ηλεκτρόνιο θα έχει μέτρο F=3,2 x 10-14 N (e=1,6 x 10-19 C), η επιτάχυνση θα είναι α=3,5 x 1016 m/s2 (me=9,1 x 10-31 kg), ο χρόνος για να φτάσει στον απέναντι οπλισμό t1 = 5,3 x 10-10s και η τελική του ταχύτητα υ1 =1,9 x 107 m/s
Διατάξεις που χρησιμοποιούν τον παραπάνω μηχανισμό (επιτάχυνση φορτισμένου σωματιδίου σε ομογενές ηλεκτροστατικό πεδίο) έχουν ευρεία εφαρμογή σε μια σειρά από συσκευές όπως ο φασματογράφος μάζας, ο καθοδικός σωλήνας και άλλες.
Β. Κίνηση με αρχική ταχύτητα κάθετη στις δυναμικές γραμμές
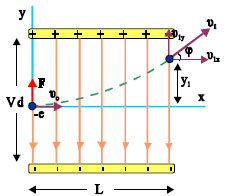
Θεωρούμε ότι οι παράλληλες μεταλλικές πλάκες του σχήματος 3.26 είναι φορτισμένες με φορτία +q και -q, έχουν μήκος L, απέχουν μεταξύ τους απόσταση d και η διαφορά δυναμικού τους είναι V. Ένα ηλεκτρόνιο εισέρχεται με αρχική ταχύτητα υ0 κάθετη στις δυναμικές γραμμές του ομογενούς πεδίου που σχηματίζεται ανάμεσα στις πλάκες. Το ηλεκτρόνιο κατά την κίνησή του μέσα στο ομογενές πεδίο δέχεται σταθερή δύναμη F.
Για τη μελέτη μιας τέτοιας κίνησης θα εφαρμόσουμε την αρχή της ανεξαρτησίας των κινήσεων.
Διαλέγουμε δύο άξονες πάνω στους οποίους αναλύουμε την κίνηση. Εδώ θα επιλέξουμε έναν άξονα παράλληλο στις δυναμικές γραμμές κι έναν κάθετο σ’ αυτές.
Αφού η διαφορά δυναμικού ανάμεσα στις φορτισμένες πλάκες είναι V, η ένταση του ηλεκτρικού πεδίου σε οποιοδήποτε σημείο του χώρου μεταξύ των πλακών
Στον άξονα x το ηλεκτρόνιο δεν δέχεται δύναμη και έτσι θα κινηθεί ευθύγραμμα ομαλά, διατηρώντας την αρχική του ταχύτητα υo .
Στον άξονα y δέχεται καθ’ όλη τη διάρκεια της κίνησης μια δύναμη σταθερή,
ηλεκτρόνιο θα εκτελέσει σ’ αυτό τον άξονα ομαλά επιταχυνόμενη κίνηση χωρίς αρχική ταχύτητα με επιτάχυνση
|
 Εικ. 3.36 To ηλεκτρόνιο εισέρχεται στο ηλεκτρικό πεδίο με ταχύτητα κάθετη στις δυναμικές γραμμές. Η δύναμη που δέχεται από το πεδίο το αναγκάζει να διαγράψει παραβολική τροχιά. Εικ. 3.36 To ηλεκτρόνιο εισέρχεται στο ηλεκτρικό πεδίο με ταχύτητα κάθετη στις δυναμικές γραμμές. Η δύναμη που δέχεται από το πεδίο το αναγκάζει να διαγράψει παραβολική τροχιά.
 Εικ. 3.2 Πειραματική διάταξη για τη μελέτη της απόκλισης μιας δέσμης ηλεκτρονίων μέσα σε ομογενές ηλεκτρικό πεδίο Εικ. 3.2 Πειραματική διάταξη για τη μελέτη της απόκλισης μιας δέσμης ηλεκτρονίων μέσα σε ομογενές ηλεκτρικό πεδίο
|
 Σχ. 3.27 Όταν το ηλεκτρόνιο εξέρχεται από το πεδίο έχει αποκλίνει κατά y1 από την αρχική του διεύθυνση και η ταχύτητα του είναι συνισταμένη της αρχικής ταχύτητας υο και της ταχύτητας υ1y. Σχ. 3.27 Όταν το ηλεκτρόνιο εξέρχεται από το πεδίο έχει αποκλίνει κατά y1 από την αρχική του διεύθυνση και η ταχύτητα του είναι συνισταμένη της αρχικής ταχύτητας υο και της ταχύτητας υ1y. |
Τελικά, στον άξονα x θα ισχύουν:
Από τις σχέσεις αυτές μπορούν να υπολογισθούν:
1. Χρόνος παραμονής στο πεδίο
Το ηλεκτρόνιο θα εξέλθει από το πεδίο όταν, στον άξονα x θα έχει μετατοπιστεί κατά L. Αν στην σχέση (3.32) θέσουμε όπου x το L και λύσουμε ως προς t προκύπτει:
2. Απόκλιση από την αρχική διεύθυνση κίνησης στην έξοδο
Εάν στη σχέση (3.34) θέσουμε στη θέση του t το χρόνο παραμονής στο πεδίο βρίσκουμε την κατακόρυφη απόκλιση y του ηλεκτρονίου από την αρχική του θέση, κατά την έξοδό του από το πεδίο.
3. Ταχύτητα εξόδου από το πεδίο
Κατά την έξοδό του από το πεδίο, η ταχύτητα του ηλεκτρονίου στον άξονα x θα είναι υ1x = υo ενώ στον y θα είναι υ1y = ayt1 και από τις (3.30) και (3.35)
H ταχύτητα που θα έχει το ηλεκτρόνιο κατά την έξοδό του θα είναι
4. Η εξίσωση της τροχιάς του ηλεκτρονίου
Η εξίσωση της τροχιάς του ηλεκτρονίου είναι η σχέση που συνδέει τις μετατοπίσεις του στους άξονες x και y. Λύνουμε την (3.32) ως προς t και αντικαθιστούμε στην (3.34) λαμβάνοντας υπόψη και την (3.30). Βρίσκουμε έτσι μια σχέση y = f (x) |
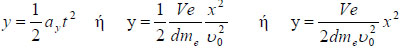
Πρόκειται για μια σχέση της μορφής y = αx2, άρα η τροχιά του ηλεκτρονίου είναι παραβολική.
Στη μελέτη της κίνησης του ηλεκτρονίου μέσα στο ομογενές ηλεκτρικό πεδίο δε λάβαμε καθόλου υπόψη το βάρος του. Αυτό έγινε γιατί το βάρος είναι αμελητέο συγκριτικά με την F. Ενδεικτικά αναφέρουμε ότι το βάρος ενός ηλεκτρονίου είναι we = 8,9 x 10-30 N ενώ η ηλεκτρική δύναμη που δέχεται ένα ηλεκτρόνιο στο εσωτερικό ενός ομογενούς ηλεκτρικού πεδίου σαν αυτό που περιγράψαμε με διαφορά δυναμικού V=1 kV και απόσταση μεταξύ των πλακών d=5mm είναι F=3,2 10-14 Ν, δηλαδή 36 x 1014 φορές μεγαλύτερη του βάρους. To συμπέρασμα αυτό, ότι το βάρος είναι αμελητέο συγκρινόμενο με την ηλεκτρική δύναμη, ισχύει και για τα άλλα στοιχειώδη σωματίδια -πρωτόνια, πυρήνες, ιόντα- όταν κινούνται μέσα στο ηλεκτρικό πεδίο.
|
|
ΠΑΡΑΔΕΙΓΜΑ 3.7 |
|||||||||||||||||||||||||||||||||
Δέσμη ηλεκτρονίων επιταχύνεται από την ηρεμία από διαφορά δυναμικού Vo. Στη συνέχεια μπαίνει σε ομογενές ηλεκτρικό πεδίο που σχηματίζεται ανάμεσα σε δυο φορτισμένες πλάκες (πλακίδια απόκλισης) κάθετα στις δυναμικές γραμμές του πεδίου. Η διαφορά δυναμικού ανάμεσα στις πλάκες είναι V και η μεταξύ τους απόσταση d. To μήκος των πλακών είναι L. Τα ηλεκτρόνια βγαίνοντας από το ομογενές πεδίο προσκρούουν σε φθορίζουσα οθόνη που είναι τοποθετημένη κάθετα στην αρχική διεύθυνση κίνησης. Η οθόνη απέχει απόσταση D από τα πλακίδια απόκλισης. Η όλη διάταξη βρίσκεται μέσα σ’ ένα σωλήνα υψηλού κενού ώστε να αποφεύγονται οι συγκρούσεις των ηλεκτρονίων με τα μόρια του αέρα. Να βρεθεί η θέση στην οποία θα πέσει η δέσμη πάνω στη φθορίζουσα οθόνη. Δίνονται το στοιχειώδες φορτίο e και η μάζα του ηλεκτρονίου me.
Ο συντελεστής απόδοσης μιας μηχανής δίνεται από την σχέση (2.18)
Η κίνηση των ηλεκτρονίων μέσα στο ηλεκτρικό πεδίο που δημιουργούν τα πλακίδια απόκλισης, μελετήθηκε στην προηγούμενη παράγραφο. Όταν τα ηλεκτρόνια εξέλθουν από τα πλακίδια απόκλισης θα έχουν εκτραπεί από την αρχική τους πορεία κατά y1. H απόκλιση αυτή υπολογίστηκε στην (3.36) επομένως
Η γωνία που σχηματίζει η ταχύτητα εξόδου των ηλεκτρονίων με την αρχική διεύθυνση κίνησης, επίσης υπολογίστηκε από τη σχέση
Τα ηλεκτρόνια βγαίνοντας από το ομογενές πεδίο των πλακιδίων κινούνται ευθύγραμμα ομαλά με υ1. Μεγεθύνοντας την περιοχή εξόδου (σχ. 3.29) βλέπουμε ότι σχηματίζεται ένα ορθογώνιο τρίγωνο με κάθετες πλευρές τις D και y2 και υποτείνουσα την τροχιά των ηλεκτρονίων. Ισχύει
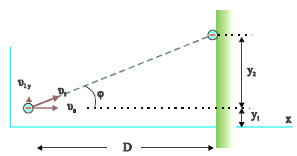 Σχ. 3.29 Σχ. 3.29
Αντικαθιστώντας την (3.40) βρίσκουμε
Η θέση της δέσμης στην οθόνη απέχει απόσταση y1+y2 από την αρχική διεύθυνση της δέσμης. Από τις (3.38), (3,39) και (3.41) βρίσκουμε:
|
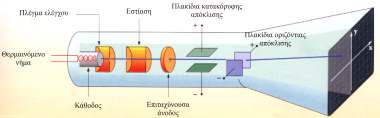
Ο ΚΑΘΟΔΙΚΟΣ ΣΩΛΗΝΑΣ
Ο καθοδικός σωλήνας, (σχ. 3.30), είναι ένας γυάλινος "σωλήνας" το εσωτερικό του οποίου βρίσκεται σε υψηλό κενό. H λειτουργία του στηρίζεται σε τρεις διαδοχικές διατάξεις. Η πρώτη ονομάζεται τηλεβόλο ηλεκτρονίων και είναι υπεύθυνη για την παραγωγή, επιτάχυνση και εστίαση μιας δέσμης ηλεκτρονίων. Η δεύτερη είναι ένας συνδυασμός ομογενών πεδίων. Μεταβάλλοντας την ένταση των πεδίων κατευθύνουμε τη δέσμη των ηλεκτρονίων. Η τρίτη είναι η οθόνη στην οποία παρατηρούμε τη θέση όπου προσπίπτουν τα ηλεκτρόνια. Ο σωλήνας απέναντι από το τηλεβόλο είναι επιστρωμένος με ειδικό υλικό που έχει την ιδιότητα να φθορίζει, δηλαδή να εκπέμπει φως, όταν πάνω του προσπίπτουν σωματίδια με μεγάλη ταχύτητα. Πάνω σ΄ αυτό το τμήμα του σωλήνα, που αποτελεί την οθόνη, πέφτουν με μεγάλη ταχύτητα τα ηλεκτρόνια της δέσμης. Στο σημείο στο οποίο πέφτουν τα ηλεκτρόνια η οθόνη φθορίζει έντονα και δημιουργείται μια φωτεινή κηλίδα.
 Σχ. 3.30 Σχ. 3.30
Στο αριστερό άκρο του σχήματος 3.30 φαίνεται το τηλεβόλο. Τα ηλεκτρόνια παράγονται εκεί με τη θέρμανση ενός μεταλλικού νήματος (κάθοδος). Θερμαίνοντας ένα μέταλλο δίνουμε σε κάποια από τα ελεύθερα ηλεκτρόνιά του κινητική ενέργεια αρκετή για να το εγκαταλείψουν. Στη συνέχεια τα ηλεκτρόνια επιταχύνονται από το ηλεκτρικό πεδίο που δημιουργείται ανάμεσα στην κάθοδο και σε ένα άλλο ηλεκτρόδιο (άνοδος). Η άνοδος βρίσκεται σε δυναμικό υψηλότερο από το δυναμικό της καθόδου και φέρει οπή. Τα περισσότερα ηλεκτρόνια που επιταχύνονται προς την άνοδο προσκρούουν σ΄ αυτή. Όσα από αυτά περνάνε από την οπή σχηματίζουν δέσμη και κινούνται προς την οθόνη με την οριζόντια ταχύτητα που απέκτησαν. Η διαφορά δυναμικού μεταξύ ανόδου και καθόδου είναι μερικά kV. Έτσι, η ταχύτητα που αποκτούν τα ηλεκτρόνια είναι της τάξεως των 107 m/s.
Στο τηλεβόλο, υπάρχουν διατάξεις που επιτρέπουν τον έλεγχο του αριθμού των ηλεκτρονίων που κατευθύνονται προς την οθόνη και την εστίαση της δέσμης.
Το εσωτερικό του καθοδικού σωλήνα βρίσκεται σε υψηλό κενό (περίπoυ 10-7 atm). Έτσι ελαχιστοποιούνται οι κρούσεις των ηλεκτρονίων της δέσμης με τα μόρια του αέρα που περιέχονται σ’ αυτόν. |
 Εικ. 3.3 Τηλεβόλο ηλεκτρονίων. Εικ. 3.3 Τηλεβόλο ηλεκτρονίων. |
 Εικ. 3.4 Παλμογράφος. Εικ. 3.4 Παλμογράφος.
 Σχ. 3.31 Εναλλασσόμενη τάση. Σχ. 3.31 Εναλλασσόμενη τάση.
 Σχ. 3.32 Πριονωτή τάση. Σχ. 3.32 Πριονωτή τάση. |
Η δέσμη των ηλεκτρονίων διέρχεται στη συνέχεια ανάμεσα από δύο ζεύγη μεταλλικών πλακιδίων (πλακίδια απόκλισης). Στο ένα ζεύγος τα μεταλλικά πλακίδια είναι οριζόντια και το ηλεκτρικό πεδίο που δημιουργείται ανάμεσά τους εκτρέπει τη δέσμη των ηλεκτρονίων κατακόρυφα. Το άλλο ζεύγος πλακιδίων είναι κατακόρυφο και εκτρέπει τη δέσμη των ηλεκτρονίων οριζόντια. Οι σχέσεις (3.39), (3.41) δείχνουν ότι η απόκλιση είναι ανάλογη της διαφοράς δυναμικού που εφαρμόζεται μεταξύ των πλακιδίων. Έτσι το σημείο της οθόνης στο οποίο προσπίπτει η δέσμη εξαρτάται από τις τάσεις που εφαρμόζουμε σε κάθε χρονική στιγμή στα δύο ζεύγη πλακιδίων. Εάν η διαφορά δυναμικού και στα δύο ζεύγη πλακιδίων απόκλισης είναι μηδενική τα ηλεκτρόνια της δέσμης κινούνται χωρίς να αποκλίνουν από την ευθύγραμμη τροχιά τους και προσκρούουν στο κέντρο της οθόνης.
Μετά την έξοδο από τα πεδία των πλακιδίων απόκλισης και μέχρι την πρόσκρουση στη φθορίζουσα οθόνη τα ηλεκτρόνια κινούνται ευθύγραμμα ομαλά.
Ο καθοδικός σωλήνας αποτελεί το βασικό στοιχείο του παλμογράφου. Πιο σύνθετες παραλλαγές του, πάνω όμως στην ίδια αρχή λειτουργίας, αποτελούν οι οθόνες της τηλεόρασης και του υπολογιστή.
ΠΑΛΜΟΓΡΑΦΟΣ
Μια ειδική εφαρμογή του καθοδικού σωλήνα είναι ο παλμογράφος. Το κύριο στοιχείο ενός παλμογράφου είναι ένας καθοδικός σωλήνας του οποίου η οθόνη είναι βαθμολογημένη ώστε να μας επιτρέπει να κάνουμε μετρήσεις. Εξωτερικά ο παλμογράφος είναι ένα κουτί με μια οθόνη στην μπροστινή πλευρά και διάφορους ρυθμιστές (κουμπιά). Με τους ρυθμιστές υπάρχει η δυνατότητα:
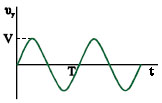
Εάν μεταξύ των πλακιδίων κατακόρυφης εκτροπής εφαρμόσουμε μια τάση που μεταβάλλεται με τον χρόνο, έστω μια τάση της μορφής υy=V ημωt (εναλλασσόμενη τάση) (σχ. 3.31) και στα πλακίδια οριζόντιας εκτροπής δεν εφαρμόζεται τάση η φωτεινή κηλίδα θα κινείται πάνω- κάτω σύμφωνα με τις αυξομειώσεις της υy. Για εναλλασσόμενες τάσεις όπως αυτή του δικτύου της ΔΕΗ η κηλίδα κινείται τόσο γρήγορα (50 φορές το δευτερόλεπτο) ώστε το μάτι να τη βλέπει σαν μια κατακόρυφη γραμμή.
Τάση σάρωσης
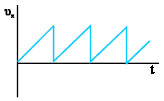
Εάν μεταξύ των πλακιδίων οριζόντιας εκτροπής εφαρμόσουμε τάση υx η οποία αυξάνεται γραμμικά και στη συνέχεια ελαττώνεται απότομα (πριονωτή τάση σχ. 3.32) η κηλίδα στην οθόνη θα κινείται οριζόντια και ισοταχώς από τα αριστερά προς τα δεξιά και θα επιστρέφει απότομα πίσω, για |
να ξαναρχίσει πάλι την ίδια κίνηση. Αυτή η παλινδρομική οριζόντια κίνηση της κηλίδας ονομάζεται σάρωση της οθόνης. Την τάση σάρωσης την εφαρμόζει ο ίδιος ο παλμογράφος και υπάρχει δυνατότητα ρύθμισης της συχνότητα της υx ώστε να επιτυγχάνουμε γρήγορη ή αργή σάρωση.
Μερικές από τις πιο απλές χρήσεις του παλμογράφου είναι.
α) Μέτρηση συνεχούς τάσεως
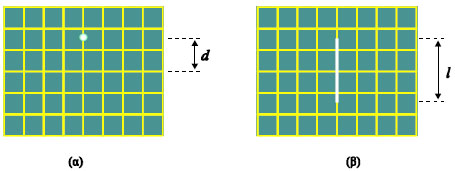
Απενεργοποιούμε την τάση σάρωσης και εφαρμόζουμε την τάση V που θέλουμε να μετρήσουμε στα πλακίδια κατακόρυφης απόκλισης. Η κηλίδα αποκλίνει κατακόρυφα (σχ. 3.33α). Από την απόσταση της κηλίδας από το κέντρο της οθόνης μπορούμε να βρούμε την εφαρμοζόμενη συνεχή τάση V.
β) Μέτρηση εναλλασσόμενης τάσης
Απενεργοποιούμε την τάση σάρωσης και στα πλακίδια κατακόρυφης απόκλισης εφαρμόζουμε τάση της μορφής υy=Vημωt (εναλλασσόμενη τάση) (σχ. 3.31). Η κηλίδα θα ανεβοκατεβαίνει γρήγορα κατακόρυφα και στην οθόνη του παλμογράφου θα σχηματιστεί μια κατακόρυφη γραμμή (σχ. 3.33β). Από το μήκος της γραμμής μπορούμε να υπολογίσουμε το V (πλάτος της εναλλασσόμενης τάσης). Συγκεκριμένα το μήκος της γραμμής είναι ανάλογο του 2V.
γ) Μελέτη κυματομορφών
Εφαρμόζουμε ταυτόχρονα τη υx (τάση σάρωσης), στα πλακίδια οριζόντιας απόκλισης και τη υy (εναλλασσόμενη) στα πλακίδια κατακόρυφης απόκλισης. Αυτό που προκύπτει στην οθόνη είναι μια κυματοειδής γραμμή (εικ. 3.5) που ονομάζεται κυματομορφή της τάσης υy. Μπορούμε έτσι να παρακολουθήσουμε στην οθόνη του παλμογράφου και να μελετήσουμε τάσεις που μεταβάλλονται με το χρόνο, όπως η εναλλασσόμενη αλλά και πιο σύνθετες.
Επειδή τα ηλεκτρόνια έχουν πολύ μικρή μάζα, η απόκλιση της δέσμης των ηλεκτρονίων στον καθοδικό σωλήνα συμβαίνει σχεδόν ακαριαία και ο παλμογράφος έχει τη δυνατότητα να δείξει πολύ γρήγορες μεταβολές στην τάση. |
Σχ. 3.33 (α) Συνεχής τάση V εφαρμόζεται στα πλακίδια κατακόρυφης απόκλισης, η απόσταση d της κηλίδας από το κέντρο της οθόνης είναι ανάλογη της τάση V. β) Εναλλασσόμενη τάση εφαρμόζεται στα πλακίδια κατακόρυφης απόκλισης, το μήκος της γραμμής στην οθόνη είναι ανάλογο του διπλάσιου πλάτους της εναλλασσόμενης τάσης.
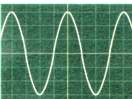 Σχ. 3.33 (Η κυματομορφή μιας εναλλασσόμενης τάσης όπως φαίνεται στην οθόνη του παλμογράφου. Σχ. 3.33 (Η κυματομορφή μιας εναλλασσόμενης τάσης όπως φαίνεται στην οθόνη του παλμογράφου. |
 Σχ. 3.34 Ένας πυκνωτής αποτελείται από δύο γειτονικούς αγωγούς φορτισμένους. Οι αγωγοί φορτίζονται με φορτία +Q και –Q. Σχ. 3.34 Ένας πυκνωτής αποτελείται από δύο γειτονικούς αγωγούς φορτισμένους. Οι αγωγοί φορτίζονται με φορτία +Q και –Q.
 Εικ. 3.6 Τύποι πυκνωτών. Εικ. 3.6 Τύποι πυκνωτών.
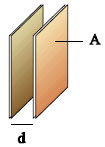 Σχ. 3.35 Επίπεδος πυκνωτής Σχ. 3.35 Επίπεδος πυκνωτής
|
3-9 ΠΥΚΝΩΤΗΣ ΚΑΙ ΧΩΡΗΤΙΚΟΤΗΤΑ
Ο πυκνωτής είναι μια διάταξη που αποθηκεύει ηλεκτρικό φορτίο και ηλεκτρική δυναμική ενέργεια. Ένας πυκνωτής αποτελείται από δύο αγωγούς που βρίσκονται κοντά και χωρίζονται μεταξύ τους από το κενό, τον αέρα, ή από άλλο μονωτή. Οι αγωγοί του σχήματος 3.34 αποτελούν ένα πυκνωτή. Οι δύο αγωγοί που αποτελούν τον πυκνωτή ονομάζονται οπλισμοί.
Πυκνωτής ονομάζεται σύστημα δύο γειτονικών αγωγών (οπλισμοί), που χωρίζονται μεταξύ τους με κάποιο μονωτικό υλικό. Οι αγωγοί φορτίζονται με φορτία +Q και -Q.
Φορτίο του πυκνωτή ονομάζεται το θετικό φορτίο του ενός από τους οπλισμούς του, ενώ τάση του πυκνωτή, ονομάζεται η διαφορά δυναμικού V, μεταξύ των οπλισμών του. Σε έναν πυκνωτή αποθηκεύεται πολύ πιο εύκολα φορτίο, από ότι σε κάθε ένα μεμονωμένο αγωγό από αυτούς που αποτελούν τον πυκνωτή.
Σε κάθε πυκνωτή η τάση του είναι ανάλογη του φορτίου του, δηλαδή το πηλίκο του φορτίου προς την τάση είναι σταθερό. Το πηλίκο αυτό το ονομάζουμε χωρητικότητα του πυκνωτή.
Χωρητικότητα C ενός πυκνωτή ονομάζεται το σταθερό πηλίκο του φορτίου του (Q) προς την τάση του (V).
Μονάδα χωρητικότητας είναι το Farad, που συμβολίζεται με το F. 1F=1 C/V.
Ονομάζεται έτσι προς τιμήν του Michael Faraday, ο οποίος μεταξύ των άλλων, ερεύνησε και το θέμα της χωρητικότητας. Το 1Farad είναι πολύ μεγάλη χωρητικότητα. Οι χωρητικότητες των πυκνωτών που χρησιμοποιούνται στην πράξη είναι της τάξης του μικροφαράντ, (1μF=10-6F), του νανοφαράντ, (1nF=10-99F) και του πικοφαράντ, (1pF=10-12F). Οι πυκνωτές παριστάνονται με δύο μικρές παράλληλες ισοϋψείς γραμμές, με ακροδέκτες συνδεδεμένους στο μέσον τους. -||-
Υπάρχουν πολλοί τύποι πυκνωτών. Στην εικόνα 3.6 φαίνονται μερικοί από αυτούς. Συνήθως παίρνουν το όνομά τους από το σχήμα των οπλισμών τους. Ο σφαιρικός πυκνωτής αποτελείται από δύο ομόκεντρους σφαιρικούς αγωγούς και ο κυλινδρικός από δύο ομοαξονικούς κυλινδρικούς αγωγούς. Ο επίπεδος πυκνωτής αποτελείται από δύο επίπεδες παράλληλες, μεταλλικές πλάκες, ίδιας επιφάνειας Α, που απέχουν μεταξύ τους απόσταση d και βρίσκονται η μια απέναντι στην άλλη.
Η χωρητικότητα ενός επίπεδου πυκνωτή είναι ανάλογη της επιφάνειας Α των οπλισμών και αντίστροφα ανάλογη της απόστασης d μεταξύ των οπλισμών.
|
Γενικότερα η χωρητικότητα ενός πυκνωτή εξαρτάται από τα γεωμετρικά στοιχεία της διάταξης ( δηλαδή από το μέγεθος, το σχήμα, τις σχετικές θέσεις των δύο αγωγών) και από το είδος του μονωτικού υλικού (ονομάζεται και διηλεκτρικό) ανάμεσα στους οπλισμούς του.
Οι πυκνωτές αποτελούν βασικά στοιχεία των ηλεκτρικών και ηλεκτρονικών κυκλωμάτων. Όταν γυρίζουμε το κουμπί του ραδιοφώνου για να επιλέξουμε σταθμό μεταβάλλουμε τη χωρητικότητα ενός πυκνωτή. Το φως που εκπέμπει το φλας της φωτογραφικής μηχανής προέρχεται από την εκφόρτιση ενός πυκνωτή. Οι πυκνωτές χρησιμοποιούνται ακόμα στους καθοδικούς σωλήνες, στα τσιπ των υπολογιστών και σε χιλιάδες άλλες εφαρμογές.
|
 Εικ. 3.7 Η λειτουργία του φλας της φωτογραφικής μηχανής στηρίζεται στην εκφόρτιση ενός πυκνωτή δια μέσου μιας λυχνίας ξένου. Καθώς εκφορτίζεται ο πυκνωτής το αέριο ξένο ιονίζεται με αποτέλεσμα την έντονη αναλαμπή μικρής διάρκειας. Εικ. 3.7 Η λειτουργία του φλας της φωτογραφικής μηχανής στηρίζεται στην εκφόρτιση ενός πυκνωτή δια μέσου μιας λυχνίας ξένου. Καθώς εκφορτίζεται ο πυκνωτής το αέριο ξένο ιονίζεται με αποτέλεσμα την έντονη αναλαμπή μικρής διάρκειας. |
ΠΑΡΑΔΕΙΓΜΑ 3.8 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Οι οπλισμοί ενός επίπεδου πυκνωτή έχουν επιφάνεια Α=4cm2 και η απόσταση τους είναι d=2mm. α) Τη χωρητικότητά του. β) Το φορτίο που θα αποκτήσει ο πυκνωτής αν συνδεθεί σε πηγή τάσης V=12V. Δίνεται εo= 8,85 x 10-12 C2 / (N m2) Απάντηση:
Η χωρητικότητα ενός επίπεδου πυκνωτή δίνεται από τη σχέση:
από την οποία, με αντικατάσταση, βρίσκουμε:
To φορτίο του πυκνωτή, όταν συνδεθεί με την πηγή, θα είναι:
ΠΑΡΑΔΕΙΓΜΑ 3.9
Ένας επίπεδος πυκνωτής έχει χωρητικότητα 10μF και φορτίζεται σε πηγή με τάση V=100V. Στη συνέχεια, αφού αποσυνδεθεί από την πηγή, οι οπλισμοί του απομακρύνονται έως ότου η απόσταση μεταξύ τους διπλασιαστεί. Να υπολογιστούν: α) η νέα χωρητικότητα του πυκνωτή και β) η τάση του μετά την απομάκρυνση των οπλισμών του. Απάντηση:
Η αρχική χωρητικότητα του πυκνωτή υπολογίζεται από τη σχέση
Όταν διπλασιάσουμε την απόσταση των οπλισμών του, η χωρητικότητά του γίνεται
Διαιρώντας κατά μέλη τις σχέσεις (3.43) και (3.42) παίρνουμε:
To φορτίο στους οπλισμούς του θα παραμείνει ίδιο και μετά την απομάκρυνση των οπλισμών. Εφόσον ο πυκνωτής δε συνδέεται με κάποιο κύκλωμα οι οπλισμοί του είναι απομονωμένοι αγωγοί και θα διατηρήσουν το φορτίο τους. Αφού με την απομάκρυνση των οπλισμών η χωρητικότητα μεταβάλλεται, αλλά το φορτίο μένει το ίδιο, θα αλλάξει η τάση στους οπλισμούς του πυκνωτή. Αν η νέα τάση του πυκνωτή είναι V΄ μπορούμε να γράψουμε
Πριν την απομάκρυνση των οπλισμών του, η χωρητικότητα του πυκνωτή ήταν:
Διαιρώντας κατά μέλη τις σχέσεις (3.45) και (3.44) παίρνουμε:
|
|
3-10 ΕΝΕΡΓΕΙΑ ΑΠΟΘΗΚΕΥΜΕΝΗ ΣΕ ΦΟΡΤΙΣΜΕΝΟ
ΠΥΚΝΩΤΗ
Σε προηγούμενη παράγραφο είδαμε ότι όλες οι διατάξεις φορτίου έχουν ορισμένη ηλεκτρική δυναμική ενέργεια U, ίση με το έργο που απαιτείται για να τοποθετηθούν τα φορτία στις θέσεις τους. Ένας φορτισμένος πυκνωτής έχει δυναμική ενέργεια U η οποία δίνεται από τη σχέση.
Η ενέργεια του φορτισμένου πυκνωτή αποδίδεται κατά την εκφόρτισή του. Αν ενώσουμε τους δύο οπλισμούς του πυκνωτή με ένα αγωγό θα μετακινηθούν φορτία από τον ένα οπλισμό στον άλλο μέχρι οι δύο οπλισμοί να αποκτήσουν το ίδιο δυναμικό. Τότε λέμε ότι ο πυκνωτής εκφορτίστηκε. Κατά την εκφόρτιση του πυκνωτή η αποθηκευμένη ηλεκτρική δυναμική ενέργεια μετατρέπεται σε θερμότητα στον αγωγό που συνδέει τους οπλισμούς. |
Υπολογισμός της ενέργειας φορτισμένου πυκνωτή Για να υπολογίσουμε τη δυναμική ενέργεια που έχει αποθηκευμένη ένας φορτισμένος πυκνωτής, ας φανταστούμε μια υποθετική διαδικασία φόρτισης: Σε ένα αρχικά αφόρτιστο πυκνωτή παίρνουμε μικρές ποσότητες φορτίου +dq από τον ένα οπλισμό και τις τοποθετούμε στον άλλο. Ο οπλισμός από τον οποίο αφαιρείται θετικό φορτίο θα φορτιστεί αρνητικά ενώ ο οπλισμός στον οποίο προσθέτουμε θετικό φορτίο, θα φορτιστεί θετικά. Έστω qo, και Vo οι τελικές τιμές για το φορτίο και την τάση του πυκνωτή. Η μεταφορά του πρώτου φορτίου dq από τον ένα οπλισμό στον άλλο γίνεται χωρίς να καταναλώσουμε έργο. Με την απόσπαση όμως του πρώτου φορτίου +dq από τον ένα οπλισμό και την εγκατάστασή του στον άλλο, ο πρώτος οπλισμός θα έχει φορτίο –dq και ο δεύτερος +dq. Aυτό θα έχει ως αποτέλεσμα τη δημιουργία πεδίου. Τώρα πια, η μεταφορά νέου φορτίου dq απαιτεί προσπάθεια (έργο), εξ αιτίας της δύναμης dF΄=Edq που ασκεί το πεδίο στο φορτίο. Η δύναμη dF που μετακινεί το φορτίο πρέπει να εξουδετερώσει τη δύναμη dF΄ του πεδίου. Όσο προχωράει η φόρτιση του πυκνωτή, το ηλεκτρικό του πεδίο θα γίνεται πιο ισχυρό και θα απαιτείται ολοένα και μεγαλύτερο έργο για τη μετακίνηση φορτίου dq. Το έργο της δύναμης dF είναι θετικό και ίσο απολύτως με το έργο της δύναμης dF΄ του πεδίου. Αν κάποια στιγμή η τάση του πυκνωτή είναι V, το έργο της δύναμης που απαιτείται για τη μετακίνηση φορτίου dq, από τον ένα οπλισμό στον άλλο είναι
Η γραφική παράσταση της σχέσης V = f(q) από την στιγμή που το φορτίο του πυκνωτή είναι μηδέν μέχρι να αποκτήσει την τελική του τιμή qo, είναι ευθεία που περνάει από την αρχή των αξόνων (σχ. 3.37). Από τη γραφική παράσταση παρατηρούμε ότι αν το σχήμα με το μπλε χρώμα μπορεί να θεωρηθεί παραλληλόγραμμο -και μπορεί να θεωρηθεί αν το dq είναι απειροστά μικρό- το εμβαδόν του θα είναι ίσο με V. dq και θα δίνει το έργο που απαιτείται για τη μεταφορά του φορτίου dq. To συνολικό έργο που απαιτείται για να φορτιστεί ο πυκνωτής θα είναι ίσο με το εμβαδόν του τριγώνου από την γραμμή του διαγράμματος μέχρι τον άξονα q, δηλαδή
Επομένως η δυναμική ενέργεια του φορτισμένου πυκνωτή είναι
|
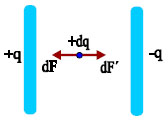 Σχ. 3.36 Ο πυκνωτής φορτίζεται με την μεταφορά απειροστά μικρών φορτίων dq από τον ένα οπλισμό στον άλλο. Σχ. 3.36 Ο πυκνωτής φορτίζεται με την μεταφορά απειροστά μικρών φορτίων dq από τον ένα οπλισμό στον άλλο.
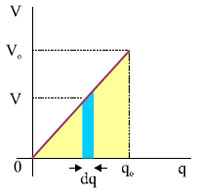 Σχ. 3.37 Από τη γραφική παράσταση της σχέσης V=q/C μπορούμε να υπολογίσουμε την ενέργεια του πυκνωτή. Σχ. 3.37 Από τη γραφική παράσταση της σχέσης V=q/C μπορούμε να υπολογίσουμε την ενέργεια του πυκνωτή. |
ΠΑΡΑΔΕΙΓΜΑ 3.10
Πυκνωτής χωρητικότητας C1=4μF, φορτίζεται από την πηγή, τάσης V=20V, με φορτίο Q. Στη συνέχεια ο πυκνωτής αποσυνδέεται από την πηγή και συνδέεται με αφόρτιστο πυκνωτή χωρητικότητας C2=12μF όπως στο σχήμα 3.39: |
Απάντηση:
Ο πυκνωτής χωρητικότητας C1, κατά τη σύνδεσή του με την πηγή απέκτησε φορτίο
Μετά την αποσύνδεση της πηγής και τη σύνδεση των δύο πυκνωτών μεταξύ τους, ένα μέρος του φορτίου Q μετακινείται ώστε να φορτιστεί και ο πυκνωτής C2. Οι πυκνωτές C1 και C2 αποκτούν φορτία Q1 και Q2, αντίστοιχα και η ( κοινή) διαφορά δυναμικού στους οπλισμούς γίνεται V΄.
Η θερμότητα που δαπανάται για κάθε κύκλο λειτουργίας της μηχανής θα υπολογιστεί από τη σχέση (2.17)
Το αρνητικό πρόσημο σημαίνει ότι η ενέργεια του συστήματος ελαττώθηκε. Η ηλεκτρική ενέργεια που χάθηκε από το σύστημα έγινε θερμότητα στους αγωγούς κατά τη μετακίνηση φορτίου από τον ένα πυκνωτή στον άλλο. |
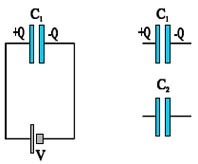 Σχ. 3.38 Σχ. 3.38
 Σχ. 3.39 Σχ. 3.39
|
3-11 ΠΥΚΝΩΤΕΣ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ
Διηλεκτρικά ή μονωτές ονομάζονται τα υλικά όπως το λάδι, το γυαλί, το λαδόχαρτο κ.ά., που δεν επιτρέπουν την κίνηση ηλεκτρικών φορτίων στο εσωτερικό τους. Οι περισσότεροι πυκνωτές έχουν ένα διηλεκτρικό ανάμεσα στους οπλισμούς τους. Ένας συνηθισμένος τύπος πυκνωτή αποτελείται από δύο μακριές λουρίδες μεταλλικών φύλλων, που είναι οι οπλισμοί, ανάμεσα στις οποίες βρίσκεται ένα φύλλο πλαστικού. Ένα τέτοιο σύστημα ΄΄σάντουιτς΄΄(σχ. 3.40) τυλίγεται σε μορφή ρολού και ο πυκνωτής που δημιουργείται με αυτόν τον τρόπο μπορεί να έχει χωρητικότητα αρκετά μικροφαράντ.
Η τοποθέτηση διηλεκτρικού μεταξύ των οπλισμών ενός πυκνωτή εξυπηρετεί τρεις λειτουργίες. α) λύνει το πρόβλημα της συγκράτησης των οπλισμών του πυκνωτή σε μικρή απόσταση μεταξύ τους χωρίς να έρχονται σε επαφή (οι οπλισμοί του πυκνωτή επειδή έχουν αντίθετα φορτία, έλκονται και έχουν την τάση να ακουμπήσουν). β) πολλές φορές τα ηλεκτρικά πεδία που δημιουργούνται ανάμεσα στους οπλισμούς του πυκνωτή είναι πολύ ισχυρά και υπάρχει ο κίνδυνος να δημιουργηθεί σπινθήρας, ο οποίος καταστρέφει τον πυκνωτή. Επειδή πολλοί μονωτές αντέχουν σε ισχυρότερα πεδία από τα πεδία που αντέχει ο αέρας είναι προτιμότερη η χρήση τους. Η μέγιστη ένταση ηλεκτρικού πεδίου στην οποία αντέχει ένας μονωτής ονομάζεται διηλεκτρική αντοχή. γ) με τη χρήση διηλεκτρικού αυξάνεται η χωρητικότητα ενός πυκνωτή.
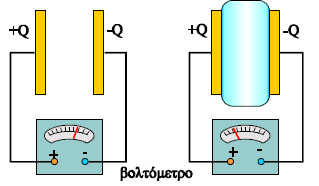
Το τελευταίο μπορούμε να το παρατηρήσουμε εύκολα ως εξής. Με ένα βολτόμετρο μετράμε τη διαφορά δυναμικού ανάμεσα στους οπλισμούς ενός φορτισμένου πυκνωτή που έχει αποσυνδεθεί από την πηγή που τον φόρτισε. Έστω ότι μας δείχνει τιμή Vo. Αν ανάμεσα στους οπλισμούς του πυκνωτή βάλουμε ένα φύλλο διηλεκτρικού -γυαλί, χαρτί, πλαστικό- η διαφορά δυναμικού παίρνει τιμή V μικρότερη από την αρχική. Όταν απομακρύνουμε το διηλεκτρικό η διαφορά δυναμικού επανέρχεται στην αρχική της τιμή Vo.
Αφού με την εισαγωγή του διηλεκτρικού η τάση ελαττώνεται ενώ το φορτίο παραμένει αμετάβλητο, η χωρητικότητα του πυκνωτή αυξάνεται. Αν η χωρητικότητα του πυκνωτή με το διηλεκτρικό είναι C ενώ χωρίς το διηλεκτρικό είναι Co, o λόγος
λέγεται διηλεκτρική σταθερά του υλικού. H διηλεκτρική σταθερά Κ είναι καθαρός αριθμός, μεγαλύτερος της μονάδας και χαρακτηρίζει το υλικό. |
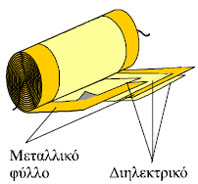 Σχ. 3.40 Πυκνωτής "σάντουιτς". Αποτελείται από δυο μεταλλικά φύλλα που διαχωρίζονται από διηλεκτρικό. Σχ. 3.40 Πυκνωτής "σάντουιτς". Αποτελείται από δυο μεταλλικά φύλλα που διαχωρίζονται από διηλεκτρικό.
Σχ. 3.41 Εάν τοποθετήσουμε διηλεκτρικό ανάμεσα στους οπλισμούς φορτισμένου πυκνωτή το βολτόμετρο δείχνει ότι η διαφορά δυναμικού μειώνεται.
|
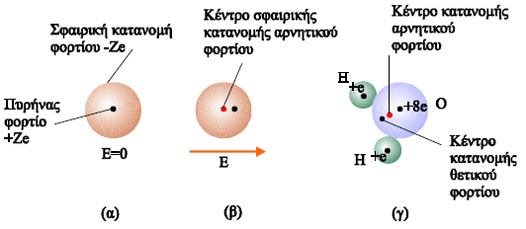
Σχ. 3.42 (α) Ένα απλό μονοατομικό μόριο εκτός ηλεκτρικού πεδίου δεν είναι δίπολο. Το κέντρο της κατανομής του αρνητικού φορτίου συμπίπτει με τον πυρήνα όπου είναι συγκεντρωμένο το θετικό φορτίο. (β) Το ίδιο μόριο όταν βρίσκεται μέσα σε ηλεκτρικό πεδίο μετατρέπεται σε δίπολο. (γ) κάποια μόρια, όπως αυτό του νερού, είναι δίπολα από την κατασκευή τους, είτε βρίσκονται σε ηλεκτρικό πεδίο είτε όχι.
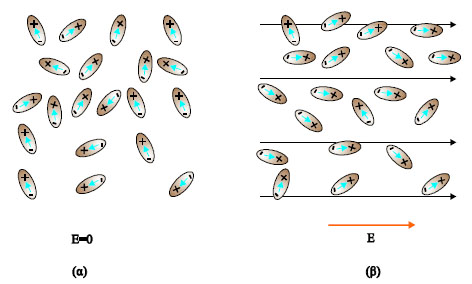
Σχ. 3.43 (α) Όταν τα δίπολα βρίσκονται εκτός ηλεκτρικού πεδίου είναι τυχαία προσανατολισμένα. (β) Τα δίπολα που βρίσκονται μέσα σε ηλεκτρικό πεδίο τείνουν να ευθυγραμμισθούν με αυτό. Η ευθυγράμμιση δεν είναι απόλυτη, λόγω της θερμικής κίνησης των μορίων.
|
Η χωρητικότητα ενός επίπεδου πυκνωτή με διηλεκτρικό είναι:
Ας δούμε όμως πού οφείλεται η αύξηση της χωρητικότητας ενός πυκνωτή όταν ανάμεσα στους οπλισμούς του τοποθετηθεί διηλεκτρικό. Από τη σχέση C = Q/V προκύπτει ότι εφ΄ όσον το φορτίο παραμένει αμετάβλητο και η χωρητικότητα αυξάνεται κατά τον παράγοντα K, με την εισαγωγή του διηλεκτρικού η τάση του πυκνωτή ελαττώνεται κατά τον ίδιο παράγοντα (K). Γνωρίζουμε ότι στο ομογενές ηλεκτρικό πεδίο ή ένταση είναι E = V/d. Αφού η τάση του πυκνωτή ελαττώνεται κατά τον παράγοντα K και η ένταση του ηλεκτρικού πεδίου μεταξύ των οπλισμών του γίνεται K φορές μικρότερη. Επομένως τα φορτία που δημιουργούν το πεδίο πρέπει να έχουν μειωθεί. Αν και το φορτίο στους οπλισμούς του πυκνωτή παραμένει αμετάβλητο, το ηλεκτρικό του πεδίο προκαλεί ανακατανομή στα φορτία του διηλεκτρικού. Το φαινόμενο ονομάζεται πόλωση. Τα μόρια του διηλεκτρικού ή είναι δίπολα ή γίνονται δίπολα όταν εισάγονται σε ηλεκτρικό πεδίο (σχ. 3.42).
Τα δίπολα αυτά προσανατολίζονται όταν βρεθούν στο ομογενές ηλεκτρικό πεδίο που δημιουργείται μεταξύ των οπλισμών του πυκνωτή (σχ. 3.43).
|
Ο προσανατολισμός των διπόλων έχει ως αποτέλεσμα η επιφάνεια του διηλεκτρικού που βρίσκεται σε επαφή με τον θετικό οπλισμό να εμφανίζει αρνητικό φορτίο και η επιφάνεια που βρίσκεται σε επαφή με τον αρνητικό οπλισμό, θετικό φορτίο (σχ. 3.44). Έτσι το συνολικό φορτίο που δημιουργεί το πεδίο είναι μικρότερο από το φορτίο που φέρουν οι οπλισμοί.

Η διηλεκτρική σταθερά και η διηλεκτρική αντοχή διαφόρων υλικών
 |
Σχ. 3.44 Το διηλεκτρικό μέσα στο ομογενές πεδίο του πυκνωτή πολώνεται. Τα επαγόμενα φορτία στις επιφάνειες του διηλεκτρικού ελαττώνουν το ηλεκτρικό πεδίο στο εσωτερικό του πυκνωτή.
Εικ. 3.8 Καταιγίδα πάνω από το Manhattan. Όταν ή ένταση του πεδίου ανάμεσα στα σύννεφα και την επιφάνεια της Γης γίνει μεγαλύτερη από τη διηλεκτρική αντοχή του αέρα ο αέρας γίνεται αγώγιμος. Με τους κεραυνούς μεγάλες ποσότητες φορτίου μεταφέρονται, μέσω του αέρα, στη Γη. Κάθε κεραυνός φέρει περίπου 1020 ηλεκτρόνια. |
ΠΑΡΑΔΕΙΓΜΑ 3.11
Μετά την εισαγωγή του διηλεκτρικού, το φορτίο του παραμένει το ίδιο, αφού ο πυκνωτής έχει αποσυνδεθεί από την πηγή, όμως η χωρητικότητα του έγινε
Αν V η τάση του πυκνωτή μετά την εισαγωγή του διηλεκτρικού είναι
Παρατηρούμε ότι η τάση του πυκνωτή είναι Κ φορές μικρότερη από την αρχική.
ΠΑΡΑΔΕΙΓΜΑ 3.12
Επίπεδος πυκνωτής με χωρητικότητα C=5μF, συνδέεται με πηγή τάσης V=10V. Χωρίς να αποσυνδέσουμε τον πυκνωτή από την πηγή, εισάγουμε ανάμεσα στους οπλισμούς του μια πλάκα διηλεκτρικού, διηλεκτρικής σταθεράς Κ=5, που καταλαμβάνει ολόκληρο το χώρο μεταξύ των οπλισμών του. Να υπολογιστεί η αύξηση του φορτίου, που προκάλεσε η εισαγωγή του διηλεκτρικού.
Επομένως η αύξηση φορτίου που προκάλεσε η εισαγωγή του διηλεκτρικού στον πυκνωτή είναι:
|
3-12 ΤΟ ΒΑΡΥΤΙΚΟ ΠΕΔΙΟ
Δύο σώματα με πολύ μικρές διαστάσεις (σημειακές μάζες), που έχουν μάζες m1 και m2 και βρίσκονται σε απόσταση r μεταξύ τους, έλκονται με δύναμη που έχει μέτρο
όπου G η σταθερά της παγκόσμιας έλξης, G = 6,673 x 10-13 N·m2 / kg2. Η δύναμη αυτή, όπως και η δύναμη Coulomb, είναι διατηρητική και κεντρική1. Η παραπάνω σχέση δίνει και τη δύναμη που αναπτύσσεται μεταξύ δύο ομογενών σφαιρικών μαζών m1 και m2. Στην περίπτωση αυτή απόσταση r είναι η απόσταση μεταξύ των κέντρων των σφαιρών και οι ελκτικές δυνάμεις έχουν σημεία εφαρμογής τα κέντρα των σφαιρών.
Η έλξη ανάμεσα σε δύο σώματα, με αίτιο το ότι έχουν μάζα, είναι δύναμη από απόσταση. Η αλληλεπίδραση μεταξύ μαζών περιγράφεται με την έννοια του πεδίου. Κάθε μάζα δημιουργεί γύρω της πεδίο. Αν κάποια μάζα βρεθεί μέσα στο πεδίο, το πεδίο τής ασκεί δύναμη.
Το πεδίο που δημιουργείται από μάζες ονομάζεται βαρυτικό πεδίο ή πεδίο βαρύτητας.
Βαρυτικό πεδίο ονομάζεται ο χώρος εκείνος στον οποίο κάθε μάζα δέχεται δύναμη.
 1 Κεντρικές λέγονται οι δυνάμεις που ασκούνται μεταξύ δύο σωμάτων και των οποίων ο φορέας συμπίπτει με την ευθεία που ενώνει τα κέντρα μάζας των σωμάτων. |
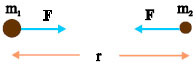 Σχ. 3.47 Δυο σημειακές μάζες που απέχουν απόσταση r έλκονται με δύναμη που είναι ανάλογη του γινομένου των μαζών και αντίστροφα ανάλογη του τετραγώνου της απόστασής τους. Σχ. 3.47 Δυο σημειακές μάζες που απέχουν απόσταση r έλκονται με δύναμη που είναι ανάλογη του γινομένου των μαζών και αντίστροφα ανάλογη του τετραγώνου της απόστασής τους.
Εικ. 3.9 Τμήμα του γαλαξία μας. Η συγκρότηση και η κίνηση των γαλαξιών οφείλεται σε βαρυτικές δυνάμεις. Η φωτεινή γραμμή που φαίνεται στη φωτογραφία είναι η τροχιά ενός μετεωρίτη που διασχίζει τη γήινη ατμόσφαιρα.
|
||||||
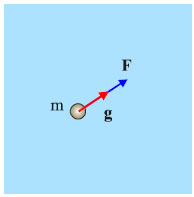 Σχ. 3.48 Εάν σ’ ένα σημείο του χώρου που καταλαμβάνει το βαρυτικό πεδίο βρεθεί μια μάζα m θα δεχθεί δύναμη. H δύναμη είναι πάντα ομόρροπη της έντασης. Σχ. 3.48 Εάν σ’ ένα σημείο του χώρου που καταλαμβάνει το βαρυτικό πεδίο βρεθεί μια μάζα m θα δεχθεί δύναμη. H δύναμη είναι πάντα ομόρροπη της έντασης.
|
Για την περιγραφή του βαρυτικού πεδίου χρησιμοποιούμε τα μεγέθη ένταση και δυναμικό.
Ένταση (g) του πεδίου βαρύτητας σε ένα του σημείο ονομάζουμε το σταθερό πηλίκο της δύναμης (F) που θα δεχτεί μια μάζα (m) αν φορτίζονται με φορτία +Q και -Q.
H ένταση έχει την ίδια κατεύθυνση με τη δύναμη. Μονάδα της έντασης είναι το 1N/kg ή 1m/s2, δηλαδή μετριέται σε μονάδες επιτάχυνσης.
Η επιτάχυνση που θα αποκτήσει ένα σώμα αν αφεθεί ελεύθερο στο πεδίο
Στο πεδίο βαρύτητας, η ένταση του πεδίου σε ένα σημείο ταυτίζεται με την επιτάχυνση που θα αποκτήσει ένα σώμα αν αφεθεί ελεύθερο σε εκείνο το σημείο. To πεδίο βαρύτητας, όπως και το ηλεκτροστατικό πεδίο, είναι διατηρητικό. Επομένως για την περιγραφή του είναι χρήσιμο το μέγεθος δυναμικό που ορίζεται με τρόπο ανάλογο. Συγκεκριμένα:
Δυναμικό (V) του πεδίου βαρύτητας, σε ένα του σημείο Α, ονομάζεται το σταθερό πηλίκο του έργου της δύναμης του πεδίου, όταν μεταφέρεται μάζα m από το σημείο Α στο άπειρο, προς τη μάζα αυτή.
Μονάδα δυναμικού του βαρυτικού πεδίου είναι το 1J/k
Διαφορά δυναμικού μεταξύ δύο σημείων Α και Β του πεδίου βαρύτητας ονομάζεται το πηλίκο του έργου της δύναμης του πεδίου, κατά τη μετακίνηση μιας μάζας m από το σημείο Α στο σημείο Β, προς τη μάζα αυτή.
Η διαφορά δυναμικού εκφράζει το έργο της δύναμης του πεδίου ανά μονάδα μάζας κατά τη μετακίνηση μιας μάζας από το σημείο Α στο σημείο Β. |
Το πεδίο που δημιουργείται από σημειακή μάζα
Η ένταση βαρυτικού πεδίου Έστω μια σημειακή μάζα Μ. Για να βρούμε την ένταση του βαρυτικού πεδίου που δημιουργεί η μάζα Μ σε σημείο Α που απέχει απόσταση r απ’ αυτήν, τοποθετούμε στο σημείο αυτό μάζα m. H μάζα m δέχεται από την μάζα Μ δύναμη
Η ένταση του πεδίου στο σημείο Α είναι
Αντικαθιστώντας την (3.53) στην (3.54) έχουμε
Το δυναμικό του βαρυτικού πεδίου που δημιουργεί η σημειακή μάζα Μ σε σημείο Α, που απέχει απόσταση r από το υλικό σημείο, έχει τιμή
Η δυναμική ενέργεια συστήματος δύο υλικών σημείων με μάζες m1, m2, που απέχουν μεταξύ τους απόσταση r, είναι ίση με το έργο που απαιτείται για να μεταφερθούν οι μάζες από πολύ μακριά και να τοποθετηθούν στις θέσεις τους και είναι
Η δυναμική ενέργεια συστήματος τριών υλικών σημείων (σχ. 3.50) υπολογίζεται με τρόπο ίδιο με αυτόν που ακολουθήσαμε στην παράγραφο 3-5. Η δυναμική ενέργεια του συστήματος είναι:
Παρατηρήσεις
|
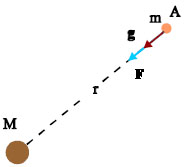 Σχ. 3.49 Η ένταση του πεδίου που δημιουργεί η σημειακή μάζα Μ έχει σε κάθε σημείο κατεύθυνση προς τη μάζα. Σχ. 3.49 Η ένταση του πεδίου που δημιουργεί η σημειακή μάζα Μ έχει σε κάθε σημείο κατεύθυνση προς τη μάζα.
 Εικ. 3.10 Το σύστημα Γη-Σελήνη Εικ. 3.10 Το σύστημα Γη-Σελήνη
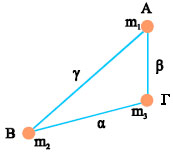 Σχ. 3.50 Σύστημα τριών υλικών σημείων. Σχ. 3.50 Σύστημα τριών υλικών σημείων. |
ΠΑΡΑΔΕΙΓΜΑ 3.13
Απάντηση:
Εφόσον οι μάζες δε δέχονται άλλες δυνάμεις εκτός από τη μεταξύ τους ελκτική δύναμη, το σύστημά τους είναι απομονωμένο και η ορμή του διατηρείται. Αν θεωρήσουμε ως αρχική θέση τη θέση όπου οι μάζες ηρεμούν και ως τελική αυτή όπου οι μάζες απέχουν μεταξύ τους απόσταση θα ισχύει:
Θεωρώντας θετική την κατεύθυνση προς τα δεξιά, η παραπάνω σχέση γράφεται
Το πεδίο βαρύτητας είναι διατηρητικό, δηλαδή η μηχανική ενέργεια του συστήματος διατηρείται σταθερή
|
3-13 ΤΟ ΒΑΡΥΤΙΚΟ ΠΕΔΙΟ ΤΗΣ ΓΗΣ
Με ικανοποιητική προσέγγιση, μπορούμε να θεωρήσουμε τη Γη σαν μια ομογενή σφαίρα ακτίνας RΓ= 6,38 x 106m και μάζας MΓ= 5,98 x 1024kg. Το βαρυτικό πεδίο της Γης σε ένα σημείο Α, στο εξωτερικό της θα περιγράφεται από τις σχέσεις (3.55) και (3.56) του πεδίου που δημιουργεί μια σημειακή μάζα. Επειδή συνήθως η θέση ενός σημείου στο πεδίο βαρύτητας της Γης προσδιορίζεται από το ύψος στο οποίο βρίσκεται το σημείο, είναι σκόπιμο στις σχέσεις αυτές να αντικαταστήσουμε την απόσταση r από το κέντρο της Γης με το άθροισμα RΓ + h όπου h το ύψος του σημείου που μας ενδιαφέρει από την επιφάνεια της Γης. Έτσι οι σχέσεις που δίνουν την ένταση και το δυναμικό στο πεδίο βαρύτητας της Γης -πάντα αναφερόμαστε στον εξωτερικό της χώρο- είναι
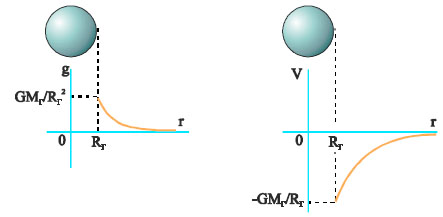
Παρατήρηση
Εάν στη σχέση της έντασης (3.59) θέσουμε h = 0 προκύπτει η ένταση του πεδίου βαρύτητας στην επιφάνεια της Γης
Με αντικατάσταση των τιμών των μεγεθών βρίσκουμε go = 9,8m/s2 |
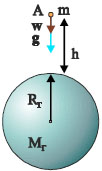 Σχ. 3.52 To σημείο Α βρίσκεται σε ύψος h, πάνω από την επιφάνεια της Γης. Σχ. 3.52 To σημείο Α βρίσκεται σε ύψος h, πάνω από την επιφάνεια της Γης.
Σχ. 3.53 Γραφικές παραστάσεις του μέτρου της έντασης και του δυναμικού σε συνάρτηση με την απόσταση από το κέντρο της Γης, για σημεία που βρίσκονται έξω από αυτή.
 Σχ. 3.11 Αστροναύτες στην επιφάνεια της Σελήνης. Παρά τον βαρύ εξοπλισμό τους (180 kg), μπορούν να κάνουν εντυπωσιακά άλματα. Στην επιφάνεια της Σελήνης η ένταση του βαρυτικού πεδίου είναι έξι φορές μικρότερη από αυτή στην επιφάνεια της Γης. Σχ. 3.11 Αστροναύτες στην επιφάνεια της Σελήνης. Παρά τον βαρύ εξοπλισμό τους (180 kg), μπορούν να κάνουν εντυπωσιακά άλματα. Στην επιφάνεια της Σελήνης η ένταση του βαρυτικού πεδίου είναι έξι φορές μικρότερη από αυτή στην επιφάνεια της Γης. |
 Εικ. 3.12 Το διαστημόπλοιο Pioneer εγκαταλείπει το βαρυτικό πεδίο της Γης. Εκτοξεύθηκε το 1973 και τώρα βρίσκεται έξω από τα όρια του ηλιακού μας συστήματος. Εικ. 3.12 Το διαστημόπλοιο Pioneer εγκαταλείπει το βαρυτικό πεδίο της Γης. Εκτοξεύθηκε το 1973 και τώρα βρίσκεται έξω από τα όρια του ηλιακού μας συστήματος.
|
3-14 ΤΑΧΥΤΗΤΑ ΔΙΑΦΥΓΗΣ – ΜΑΥΡΕΣ ΤΡΥΠΕΣ
Με ποια ταχύτητα πρέπει να εκτοξευθεί ένα αντικείμενο μάζας m, από την επιφάνεια της Γης ώστε να διαφύγει οριστικά από το πεδίο βαρύτητας της Γης;
Για να απλουστεύσουμε το πρόβλημα θα θεωρήσουμε ότι η Γη δεν κινείται, θα αγνοήσουμε τις βαρυτικές επιδράσεις από τα άλλα ουράνια σώματα και θα αγνοήσουμε την αντίσταση του ατμοσφαιρικού αέρα.
Εφόσον το βαρυτικό πεδίο είναι διατηρητικό η μηχανική ενέργεια του συστήματος των δύο σωμάτων (Γη και σώμα) διατηρείται. Επομένως κατά την κίνηση του σώματος μεταξύ δύο θέσεων θα ισχύει
Εφαρμόζουμε τη σχέση αυτή για ένα σημείο πάνω στην επιφάνεια της Γης και για το άπειρο (εκεί όπου δεν υπάρχει πλέον βαρυτική επίδραση και η δυναμική ενέργεια του συστήματος σώμα – Γη είναι μηδέν U2 = 0). Η ελάχιστη τιμή της ταχύτητας με την οποία πρέπει να εκτοξεύσουμε το σώμα είναι εκείνη για την οποία το σώμα θα φτάνει στο άπειρο με μηδενική ταχύτητα, άρα Κ2=0 Από την (3.61) έχουμε
Λύνοντας ως προς υδ βρίσκουμε
Την ταχύτητα υδ την ονομάζουμε ταχύτητα διαφυγής από την επιφάνεια της Γης.
Εάν το σημείο εκτόξευσης βρίσκεται σε ύψος h από την επιφάνεια της Γης με τον ίδιο τρόπο προκύπτει ότι η ταχύτητα διαφυγής δίνεται από τη σχέση
Ακολουθώντας την ίδια διαδικασία μπορούμε να βρούμε την ταχύτητα διαφυγής από την επιφάνεια άλλων ουράνιων σωμάτων.Έτσι για παράδειγμα για τη Σελήνη βρίσκουμε 2,37 km/s, για τον Άρη 4,97 km/s, για το Δία 59,1 km/s και για τον Ήλιο 618 km/s.
Ας δούμε τώρα το πρόβλημα της ταχύτητας διαφυγής με άλλο τρόπο. Αντί να ψάξουμε να βρούμε με ποια ταχύτητα πρέπει να εκτοξευθεί ένα σώμα από την επιφάνεια ενός ουράνιου σώματος μάζας Μ και ακτίνας R ώστε να διαφύγει από τη βαρυτική του έλξη θα βρούμε τι ακτίνα πρέπει να έχει ένα ουράνιο σώμα μάζας Μ ώστε να μην επιτρέπει σε τίποτα να διαφύγει από την επιφάνειά του. |
Η μεγαλύτερη ταχύτητα στη φύση είναι η ταχύτητα του φωτός c = 3 x 108 m/s.
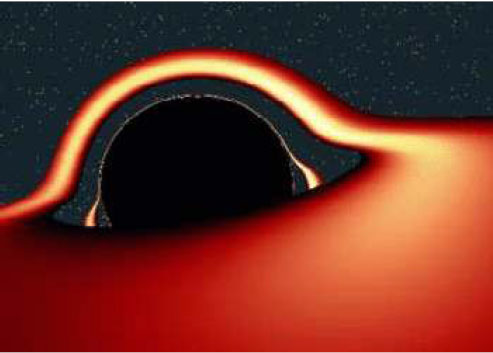
ακτίνα Schwarzschild. Ένα ουράνιο σώμα μάζας Μ με ακτίνα μικρότερη από αυτή την ακτίνα δεν επιτρέπει σε τίποτε, ούτε καν στο φως, να διαφύγει από το πεδίο βαρύτητάς του. Ένα τέτοιο σώμα δεν είναι άμεσα παρατηρήσιμο κάνει όμως αντιληπτή την παρουσία του από τις ισχυρότατες βαρυτικές έλξεις που ασκεί στον περίγυρό του. Τέτοια σώματα στη σύγχρονη φυσική χαρακτηρίζονται μαύρες τρύπες.
Οι συνθήκες που επικρατούν στην περιοχή μιας μαύρης τρύπας και οι ταχύτητες διαφυγής για τις οποίες μιλάμε είναι πολύ μακριά από αυτό που ο καθένας μας αντιλαμβάνεται σαν πραγματικότητα και δεν περιγράφονται από τους νόμους της νευτώνειας μηχανικής. Η σχέση που δίνει την ακτίνα Schwarzschild παράγεται λαμβάνοντας υπόψη τις διορθώσεις που επέφερε η θεωρία της σχετικότητας στην κλασική μηχανική. Το γεγονός όμως ότι συμπίπτει με τη σχέση που βρήκαμε για την ταχύτητα διαφυγής χρησιμοποιώντας το νόμο διατήρησης της μηχανικής ενέργειας μάς επιτρέπει μια πρώτη προσέγγιση στο φαινόμενο.
Για να αποκτήσουμε ένα μέτρο της πυκνότητας στην οποία βρίσκεται η ύλη σε μια μαύρη τρύπα αναφέρουμε ότι για να περιπέσει σε κατάσταση μαύρης τρύπας ο Ήλιος πρέπει να συμπιεσθεί σε μια σφαίρα ακτίνας 3 km, από 6,96 x 105 km που είναι σήμερα.
της θα έπρεπε να συγκεντρωθεί σ΄ ένα μπαλάκι μεγέθους ίσου με αυτό του πινγκ πονγκ.
|
Εικ. 3.13 Προσομοίωση μαύρης τρύπας σε υπολογιστή. Η ύλη έλκεται από μια μαύρη τρύπα σχηματίζοντας γύρω της ένα περιστρεφόμενο δίσκο. Τα άτομα των αερίων που σχηματίζουν το δίσκο επιταχυνόμενα αποκτούν τόση ενέργεια ώστε μετατρέπονται σε ισχυρότατες πηγές ακτίνων Χ. Σε περιοχές του σύμπαντος όπου ανιχνεύουμε ασυνήθιστα μεγάλης έντασης εκπομπή ακτινοβολίας Χ υποπτευόμαστε την ύπαρξη μιας μαύρης τρύπας. |
ΠΑΡΑΔΕΙΓΜΑ 3.14
Από το σημείο Α του πεδίου βαρύτητας της Γης, που βρίσκεται σε ύψος h=RΓ από την επιφάνεια της Γης (RΓ η ακτίνα της Γης), βάλλεται προς το Διάστημα ένα σώμα με ταχύτητα υΓ=16 x 103 m/s. Να εξετάσετε αν το σώμα θα διαφύγει από τη βαρυτική έλξη της Γης. Αν θα διαφύγει να βρείτε την ταχύτητά του όταν φτάσει σε πολύ μεγάλη απόσταση από τη Γη. Δίνονται: η ακτίνα της Γης RΓ=6400 km και η ένταση του πεδίου βαρύτητας στην επιφάνειά της go=10 m/s2. 
|
|
3-15 ΣΥΓΚΡΙΣΗ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΚΑΙ
ΒΑΡΥΤΙΚΟΥ ΠΕΔΙΟΥ
Η μαθηματική ομοιότητα ανάμεσα στο νόμο του Coulomb και το νόμο της παγκόσμιας έλξης (και οι δύο δυνάμεις είναι αντίστροφα ανάλογες με το τετράγωνο της απόστασης), καθώς και το γεγονός ότι και οι δυο είναι διατηρητικές και κεντρικές, οδηγεί σε σκέψεις ότι υπάρχουν και περαιτέρω αναλογίες ανάμεσα στα δύο πεδία. Στην πραγματικότητα όμως πρόκειται για δύο πεδία στα οποία οι διαφορές είναι περισσότερες από τις ομοιότητες. Ενδεικτικά αναφέρουμε κάποιες διαφορές.
|
ΣΥΝΟΨΗ |
|||||||||||||||||||||||||||||||||||||||||||||||||
Πεδίο ονομάζεται ο χώρος εκείνος στον οποίο αν βρεθεί το κατάλληλο κάθε φορά υπόθεμα δέχεται δύναμη. Ένταση σ’ ένα σημείο Α ενός ηλεκτροστατικού πεδίου είναι το σταθερό πηλίκο της δύναμης που ασκείται από το πεδίο σ’ ένα φορτίο q που θα βρεθεί στο σημείο Α προς το φορτίο αυτό.
Η φορά της έντασης του ηλεκτροστατικού πεδίου συμπίπτει με τη φορά της δύναμης που ασκείται σε θετικά φορτία. Το
Η ηλεκτρική ροή ΦΕ που διέρχεται από μια επίπεδη επιφάνεια, εμβαδού Α, η οποία βρίσκεται μέσα σε ομογενές ηλεκτρικό πεδίο έντασης Ε, είναι ΦΕ= ΕΑσυνθ, όπου θ η γωνία που σχηματίζει το κάθετο στην επιφάνεια διάνυσμα Α με τη διεύθυνση των δυναμικών γραμμών. Η ηλεκτρική ροή μετριέται σε μονάδες Ν m2/C. Η ηλεκτρική ροή που διέρχεται από μια κλειστή επιφάνεια ισούται με το πηλίκο του ολικού φορτίου που περικλείει η επιφάνεια, προς τη σταθερά εο. (νόμος του Gauss)
Δυναμικό του ηλεκτρικού πεδίου σε ένα του σημείο Α (συμβολίζεται VA), ονομάζεται το σταθερό πηλίκο, του έργου της δύναμης του πεδίου που ασκείται σε φορτίο q κατά τη μετακίνηση του φορτίου q από το σημείο Α στο άπειρο, προς το φορτίο που μετακινείται.
To δυναμικό είναι μονόμετρο μέγεθος και στο σύστημα SI έχει μονάδα το 1V=1 J/C. Η διαφορά δυναμικού, V A - V B, ανάμεσα σε δύο σημεία Α και Β του ηλεκτρικού πεδίου είναι ίση με το πηλίκο του έργου που παράγει ή καταναλώνει η δύναμη του πεδίου κατά τη μετακίνηση ενός φορτίου από το σημείο Α στο σημείο Β, προς το φορτίο q.
Το δυναμικό ηλεκτρικού πεδίου που δημιουργείται από ένα σημειακό φορτίο Q σε ένα σημείο του που απέχει από το Q απόσταση r, έχει τιμή
Ένας ηλεκτροστατικά φορτισμένος αγωγός έχει παντού το ίδιο δυναμικό. Η δυναμική ενέργεια συστήματος δύο σημειακών φορτίων q1 και q2 που απέχουν μεταξύ τους απόσταση r είναι
Η ένταση στο ομογενές ηλεκτρικό πεδίο είναι ίση με το πηλίκο της διαφοράς δυναμικού δύο οποιωνδήποτε σημείων του ηλεκτρικού πεδίου προς την μεταξύ τους απόσταση x, μετρημένης κατά μήκος μιας δυναμικής γραμμής.
|
Πυκνωτής ονομάζεται το σύστημα δύο γειτονικών αγωγών (οπλισμοί) που χωρίζονται μεταξύ τους με κάποιο μονωτικό υλικό. Oι αγωγοί φορτίζονται με φορτία. +Q και –Q. Οι γραμμομοριακές ειδικές θερμότητες Cp και CV για ένα αέριο έχουν σταθερό λόγο.
Μονάδα χωρητικότητας είναι το Farad (F). 1F=1 C/V.
Η χωρητικότητα ενός πυκνωτή εξαρτάται από τα γεωμετρικά στοιχεία της διάταξης (δηλαδή από το μέγεθος, το σχήμα, τις σχετικές θέσεις των δύο αγωγών) και από το είδος του μονωτικού υλικού (ονομάζεται και διηλεκτρικό) ανάμεσα στους οπλισμούς του. Η ενέργεια που έχει αποθηκευμένη ένας φορτισμένος πυκνωτής είναι
Η μέγιστη ένταση ηλεκτρικού πεδίου στην οποία αντέχει ένας μονωτής ονομάζεται διηλεκτρική αντοχή. Ονομάζουμε διηλεκτρική σταθερά Κ ενός υλικού, το λόγο της χωρητικότητας του πυκνωτή με το διηλεκτρικό προς τη χωρητικότητα του πυκνωτή χωρίς το διηλεκτρικό.
Η βαρυτική έλξη ανάμεσα σε δύο σώματα με πολύ μικρές διαστάσεις (σημειακές μάζες) που έχουν μάζες m1 και m2 και βρίσκονται σε απόσταση r μεταξύ τους, έχει μέτρο ίσο με
όπου G η σταθερά παγκοσμίου έλξεως, G = 6,673x10-11 N·m2/kg2. Η δύναμη αυτή είναι διατηρητική και κεντρική. Πεδίο βαρύτητας ονομάζεται ο χώρος εκείνος στον οποίο αν βρεθεί κάποια μάζα θα δεχτεί δύναμη.
Μονάδα της έντασης του βαρυτικού πεδίου είναι το 1N/kg ή 1m/s2. Δυναμικό (V) του πεδίου βαρύτητας σε ένα του σημείο Α, ονομάζεται το σταθερό πηλίκο του έργου της δύναμης του πεδίου κατά τη μετακίνηση μάζας m από το σημείο Α στο άπειρο, προς τη μάζα αυτή.
Μονάδα δυναμικού του βαρυτικού πεδίου είναι το 1J/kg Διαφορά δυναμικού μεταξύ δύο σημείων Α και Β του πεδίου βαρύτητας ονομάζεται το πηλίκο του έργου της δύναμης του πεδίου κατά τη μετακίνηση μιας μάζας m από το σημείο Α στο σημείο Β, προς τη μάζα αυτή.
Η ένταση σε ένα σημείο Α βαρυτικού πεδίου που δημιουργείται από μια σημειακή μάζα Μ είναι
Το δυναμικό βαρυτικού πεδίου σημειακής μάζας Μ σε σημείο Α που απέχει απόσταση r από αυτήν είναι
Η δυναμική ενέργεια συστήματος δύο σημειακών μαζών m1, m2, που απέχουν μεταξύ τους απόσταση r είναι
Ταχύτητα διαφυγής από το βαρυτικό πεδίο της Γης είναι η ελάχιστη ταχύτητα με την οποία πρέπει να εκτοξευθεί ένα σώμα από σημείο που βρίσκεται σε ύψος h από την επιφάνεια της Γης, για να διαφύγει από το βαρυτικό της πεδίο.
|
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ |
1. Το φαινόμενο της παλίρροιας
 Εικ. 3.14 Το φαινόμενο της άμπωτης και της πλημμυρίδας στον κόλπο του Fundy στον Καναδά Εικ. 3.14 Το φαινόμενο της άμπωτης και της πλημμυρίδας στον κόλπο του Fundy στον Καναδά |
ΕΡΩΤΗΣΕΙΣ |
 Σχ. 3.54 Σχ. 3.54
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ΑΣΚΗΣΕΙΣ |
|
|
|||||||||||||||
|
 Σχ. 3.55 Σχ. 3.55
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ΠΡΟΒΛΗΜΑΤΑ |
|
 Σχ. 3.56 Σχ. 3.56 |
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
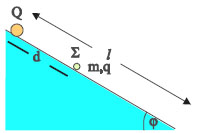 Σχ. 3.57 Σχ. 3.57 |
|||||||||||||||||||||||||||||||||
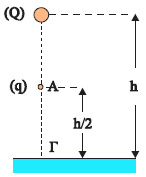 Σχ. 3.58 Σχ. 3.58
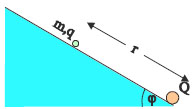 Σχ. 3.59 Σχ. 3.59
|
|
|
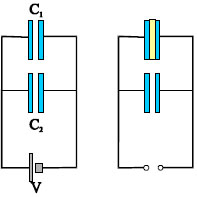 Σχ. 3.60 Σχ. 3.60
|
||||||||||||||||||||||||||||||||||||||||||||||||
 Εικ. 3.15 Ο αστροναύτης στηρίζεται στο δορυφόρο που βρίσκεται σε τροχιά Εικ. 3.15 Ο αστροναύτης στηρίζεται στο δορυφόρο που βρίσκεται σε τροχιά |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
 Εικ. 3.16 Ο Φόβος, δορυφόρος του Άρη. Εικ. 3.16 Ο Φόβος, δορυφόρος του Άρη. |
|||||||||||||||||||||||||||||||||||||||

|
TO ΠΕΙΡΑΜΑ TOY MILLIKAN Την περίοδο 1909-1913, o Robert Millikan (Μίλικαν), με ένα εμπνευσμένα απλό πείραμα που πραγματοποίησε στο πανεπιστήμιο του Σικάγου, μέτρησε για πρώτη φορά το στοιχειώδες φορτίο e και απέδειξε ότι το ηλεκτρικό φορτίο είναι κβαντισμένο -υπάρχει δηλαδή μόνο σε διακριτές ποσότητες, που είναι ακέραια πολλαπλάσια του στοιχειώδους φορτίου e.
Στο σχήμα βλέπουμε το μοντέλο της πειραματικής συσκευής του Millikan. Αποτελείται από δύο παράλληλες μεταλλικές πλάκες. Η πάνω πλάκα έχει μια μικρή τρύπα από την οποία διέρχονται μικρά σταγονίδια λαδιού. Τα σταγονίδια αυτά είναι φορτισμένα λόγω της τριβής τους με το ακροφύσιο του ψεκαστήρα με το οποίο ψεκάζεται το λάδι. Μια οριζόντια δέσμη φωτός φωτίζει τα σταγονίδια λαδιού, τα οποία μπορούν να παρατηρηθούν με ένα μικροσκόπιο. Καθώς το φως πέφτει πάνω στα σταγονίδια αυτά φαίνονται σαν λαμπερά σημεία μέσα στο σκοτάδι.
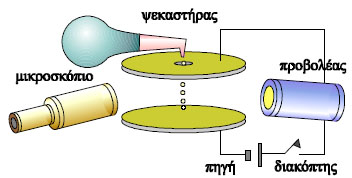 Σχ. 3.61 Το μοντέλο της συσκευής του Millikan Σχ. 3.61 Το μοντέλο της συσκευής του Millikan
Έστω ένα σταγονίδιο μάζας m που είναι φορτισμένο με αρνητικό φορτίο q, λόγω της τριβής του με το ακροφύσιο του ψεκαστήρα. Εάν δεν υπάρχει ηλεκτρικό πεδίο ανάμεσα στις πλάκες, στο σταγονίδιο δρουν δυο δυνάμεις: το βάρος του mg που κατευθύνεται προς τα κάτω, και η αντίσταση του αέρα F, που κατευθύνεται προς τα πάνω.
Η αντίσταση (F) δεν είναι σταθερή αλλά εξαρτάται από την ταχύτητα με την οποία πέφτει το σταγονίδιο. Για μικρές ταχύτητες, η αντίσταση που δέχεται στον αέρα μια μικρή σφαίρα, όπως οι σταγόνες του λαδιού, δίνεται από τη σχέση
όπου μ το ιξώδες του αέρα (ιξώδες: ένα μέγεθος που δείχνει πόσο παχύρρευστο είναι ένα ρευστό), r η ακτίνα της σταγόνας και υ η ταχύτητά της.
Όσο το βάρος mg είναι μεγαλύτερο από την αντίσταση, η σταγόνα επιταχύνεται. Καθώς όμως η ταχύτητά της αυξάνεται, μεγαλώνει η αντίσταση και σύντομα γίνεται αντίθετη με το βάρος. Τότε η σταγόνα αποκτά μια τελική, οριακή ταχύτητα.
|
Η μάζα της σταγόνας μπορεί να γραφεί, όπου η πυκνότητα και ο όγκος της σταγόνας. Ο
Οπότε η σχέση (3.65) γίνεται
Η ταχύτητα με την οποία κινείται ένα σταγονίδιο είναι μερικά εκατοστά του εκατοστού του μέτρου το δευτερόλεπτο και επομένως είναι δυνατόν να μετρηθεί, οπότε η σχέση (3.66) μας δίνει την ακτίνα της σταγόνας. Έστω τώρα ότι συνδέουμε τις δύο πλάκες με τους πόλους μιας πηγής, έτσι ώστε η επάνω πλάκα να έχει το υψηλό δυναμικό. Τώρα εκτός από τις δύο δυνάμεις που αναφέρθηκαν προηγουμένως, στο σταγονίδιο ασκείται και μια δύναμη από το πεδίο Εq. Υποθέσαμε ότι το φορτίο q είναι αρνητικό, επομένως η ηλεκτρική δύναμη κατευθύνεται προς τα πάνω. Από το μέτρο της δύναμης θα εξαρτηθεί αν το σταγονίδιο θα συνεχίσει να κινείται προς τα κάτω, με μικρότερη ταχύτητα, ή θα αντιστρέψει την κίνησή του. Όπως και να ‘χει η συνισταμένη των τριών δυνάμεων γίνεται πάλι μηδέν και τότε η σταγόνα τελικά αποκτά μια νέα οριακή ταχύτητα. Ας πάρουμε την περίπτωση όπου η ηλεκτρική δύναμη είναι αρκετά μεγάλη και το σταγονίδιο κινείται προς τα πάνω, τότε η αντίσταση F, κατευθύνεται προς τα κάτω. Αν υ΄ είναι η νέα οριακή ταχύτητα που θα αποκτήσει η σταγόνα, ισχύει
Μετρώντας την υ΄ και έχοντας ήδη υπολογίσει την ακτίνα, από την σχέση (3.66) μπορούμε να υπολογίσουμε το φορτίο q. Με μια μεγάλη σειρά μετρήσεων ο Millikan βρήκε ότι το φορτίο κάθε σταγόνας ήταν ακέραιο πολλαπλάσιο μιας στοιχειώδους ποσότητας φορτίου e. Έκανε ακόμα την υπόθεση ότι, το φορτίο αυτό ήταν ίσο, σε απόλυτη τιμή, με το φορτίο ενός ηλεκτρονίου. Η υπόθεσή του επιβεβαιώθηκε. Για την εργασία του αυτή ο Millikan τιμήθηκε το 1923 με το βραβείο Νόμπελ. |
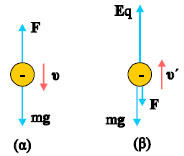 Σχ. 3.62 (α) Οι δυνάμεις στην σταγόνα που πέφτει με την οριακή της ταχύτητα υ. (β) Οι δυνάμεις παρουσία του ηλεκτρικού πεδίου. Σχ. 3.62 (α) Οι δυνάμεις στην σταγόνα που πέφτει με την οριακή της ταχύτητα υ. (β) Οι δυνάμεις παρουσία του ηλεκτρικού πεδίου. |